江苏省南京市秦淮区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
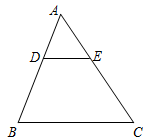
1. 方程 的解是( )A、x1=x2=2. B、x1=x2=-2. C、x1=2,x2=-2. D、x1=2,x2=4.2. 如图,在△ABC中,DE∥BC,若DE=2,BC=6,则 =( )
 A、 B、 C、 D、3. 二次函数y=3(x-2)2-1的图像顶点坐标是( )A、(-2,1) B、(-2,-1) C、(2,1) D、(2,-1)4. 如图,OA是⊙O的半径,弦BC⊥OA,D是优弧 上一点,如果∠AOB=58º,那么∠ADC的度数为( )
A、 B、 C、 D、3. 二次函数y=3(x-2)2-1的图像顶点坐标是( )A、(-2,1) B、(-2,-1) C、(2,1) D、(2,-1)4. 如图,OA是⊙O的半径,弦BC⊥OA,D是优弧 上一点,如果∠AOB=58º,那么∠ADC的度数为( )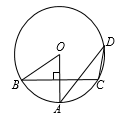 A、32º B、29º C、58º D、116º5. 某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
A、32º B、29º C、58º D、116º5. 某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )操作组
管理组
研发组
日工资(元/人)
260
280
300
人数(人)
4
4
4
A、团队平均日工资不变 B、团队日工资的方差不变 C、团队日工资的中位数不变 D、团队日工资的极差不变6. 已知二次函数y=ax2+bx+c(a<0<b)的图像与x轴只有一个交点,下列结论:①x<0时,y随x增大而增大;②a+b+c<0;③关于x的方程ax2+bx+c+2=0有两个不相等的实数根.其中所有正确结论的序号是( )A、①② B、②③ C、①③ D、①②③二、填空题
-
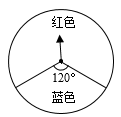
7. 在比例尺为1∶500 000的地图上,量得A、B两地的距离为3 cm,则A、B两地的实际距离为km.8. 设x1 , x2是关于x的一元二次方程x2+x-4=0的两根,则x1+x2+x1x2= .9. 如图,一个可以自由转动的转盘,任意转动转盘一次,当转盘停止时,指针落在红色区域的概率为 .
 10. 若圆锥的底面半径为3cm,高为4cm,则它的侧面展开图的面积为cm2 .11. 将二次函数y=2x2的图像向上平移3个单位长度,再向右平移2个单位长度,得到的图像所对应的函数表达式为 .12. 已知点P是线段AB的黄金分割点,PA>PB,AB=4 cm,则PA=cm.13. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=°.
10. 若圆锥的底面半径为3cm,高为4cm,则它的侧面展开图的面积为cm2 .11. 将二次函数y=2x2的图像向上平移3个单位长度,再向右平移2个单位长度,得到的图像所对应的函数表达式为 .12. 已知点P是线段AB的黄金分割点,PA>PB,AB=4 cm,则PA=cm.13. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=°.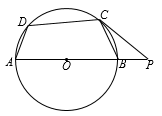 14. 二次函数y=ax2+bx+c(a≠0)的图像如图所示,当y<3时,x的取值范围是 .
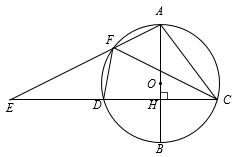
14. 二次函数y=ax2+bx+c(a≠0)的图像如图所示,当y<3时,x的取值范围是 . 15. 如图,在□ABCD中,AB=5,AD=6,AD、AB、BC分别与⊙O相切于E、F、G三点,过点C作⊙O的切线交AD于点N,切点为M.当CN⊥AD时,⊙O的半径为 .
15. 如图,在□ABCD中,AB=5,AD=6,AD、AB、BC分别与⊙O相切于E、F、G三点,过点C作⊙O的切线交AD于点N,切点为M.当CN⊥AD时,⊙O的半径为 .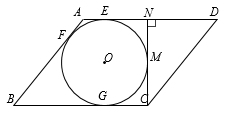 16. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .
16. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为 .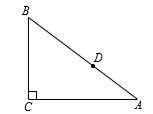
三、解答题
-
17. 解方程(1)、x2-6x-7=0;(2)、(2x-1)2=9.18. 某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
跳绳成绩(个)
132
133
134
135
136
137
一班人数(人)
1
0
1
5
2
1
二班人数(人)
0
1
4
1
2
2
(1)、两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:众数
中位数
平均数
方差
一班
a
135
135
c
二班
134
b
135
1.8
表中数据a= , b= , c=;
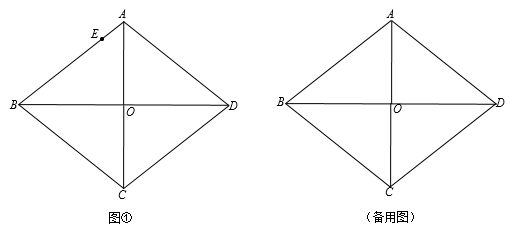
(2)、请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.19. 某校举行秋季运动会,甲、乙两人报名参加100 m比赛,预赛分A、B、C三组进行,运动员通过抽签决定分组.(1)、甲分到A组的概率为;(2)、求甲、乙恰好分到同一组的概率.20. 如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.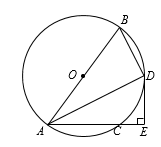 (1)、求证:DE是⊙O的切线;(2)、若BD=3,AD=4,则DE= .21. 已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:
(1)、求证:DE是⊙O的切线;(2)、若BD=3,AD=4,则DE= .21. 已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:x
…
-2
-1
0
1
2
…
y
…
5
0
-3
-4
-3
…
(1)、求该二次函数的表达式;(2)、该二次函数图象关于x轴对称的图像所对应的函数表达式为 .22. 如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE. (1)、求证:△DAC∽△EBC;(2)、求△ABC与△DEC的面积比.23. 新建马路需要在道路两旁安装路灯、种植树苗.如图,某道路一侧路灯AB在两棵同样高度的树苗CE和DF之间,树苗高2 m,两棵树苗之间的距离CD为16 m,在路灯的照射下,树苗CE的影长CG为1 m,树苗DF的影长DH为3 m,点G、C、B、D、H在一条直线上.求路灯AB的高度.
(1)、求证:△DAC∽△EBC;(2)、求△ABC与△DEC的面积比.23. 新建马路需要在道路两旁安装路灯、种植树苗.如图,某道路一侧路灯AB在两棵同样高度的树苗CE和DF之间,树苗高2 m,两棵树苗之间的距离CD为16 m,在路灯的照射下,树苗CE的影长CG为1 m,树苗DF的影长DH为3 m,点G、C、B、D、H在一条直线上.求路灯AB的高度. 24. 某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
24. 某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.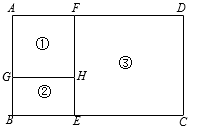 (1)、用含x的代数式表示DF=;(2)、x为何值时,区域③的面积为180平方米;(3)、x为何值时,区域③的面积最大?最大面积是多少?25. 已知二次函数y=(x-m)(x+m+4),其中m为常数.(1)、求证:不论m为何值,该二次函数的图象与x轴有公共点.(2)、若A(-1,a)和B(n,b)是该二次函数图象上的两个点,请判断a、b的大小关系.
(1)、用含x的代数式表示DF=;(2)、x为何值时,区域③的面积为180平方米;(3)、x为何值时,区域③的面积最大?最大面积是多少?25. 已知二次函数y=(x-m)(x+m+4),其中m为常数.(1)、求证:不论m为何值,该二次函数的图象与x轴有公共点.(2)、若A(-1,a)和B(n,b)是该二次函数图象上的两个点,请判断a、b的大小关系.