广西壮族自治区贺州市昭平县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-02-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次函数的开口方向一定向上的是（）

A、y=-3x²-1 B、y=- $\frac{1}{3}$ x²+1 C、y= $\frac{1}{2}$ x²+3 D、y=-x²-5

查看试题解析
2. 已知 $\frac{a}{b} = \frac{1}{2}$ ，则 $\frac{a + b}{b}$ 的值是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
3. 两个相似三角形对应高之比为 $1 : 2$ ，那么它们的对应中线之比为（）

A、 $1 : 2$ B、 $1 : 3$ C、 $1 : 4$ D、 $1 : 8$

查看试题解析
4. 下列各点在反比例函数y=- $\frac{6}{x}$ 图象上的是（）

A、(3，2) B、(2，3) C、(-3，-2) D、( - $\frac{6}{2}$ ，2 )

查看试题解析
5. 在Rt△ABC中，∠C=90°，若cosB= $\frac{1}{2}$ ，则∠B的度数是（）

A、90° B、60° C、45° D、30°

查看试题解析
6. 关于二次函数y=2x²+4，下列说法错误的是（）

A、它的开口方向向上 B、当x=0时，y有最大值4 C、它的对称轴是y轴 D、顶点坐标为(0，4)

查看试题解析
7. 如图，▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）

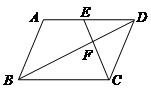A、3：2 B、3：1 C、1：1 D、1：2

查看试题解析
8. 如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4：9，则OB′：OB为（）

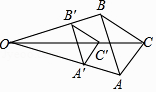A、2：3 B、3：2 C、4：5 D、4：9

查看试题解析
9. 某商场降价销售一批名牌衬衫，已知所获利润y(元)与降价x(元)之间的关系是y=-2x²+60x+800，则利润获得最多为（）

A、15元 B、400元 C、800元 D、1250元

查看试题解析
10. 如图，学校的保管室有一架5m长的梯子斜靠在墙上，此时梯子与地面所成的角为45°如果梯子底端O固定不变，顶端靠到对面墙上，此时梯子与地面所成的角为60°，则此保管室的宽度AB为（）

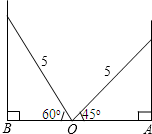A、 $\frac{5}{2}$ ( $\sqrt{2}$ +1 ) m B、 $\frac{5}{2}$ ( $\sqrt{2}$ +3 ) m C、( $3 + \sqrt{2}$ ) m D、 $\frac{5}{2}$ ( $\sqrt{3}$ +1 ) m

查看试题解析
11. 如图，在△ABC中，∠A=45°，∠C=90°，点D在线段AC上，∠BDC=60°，AD=1，则BD等于（）

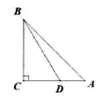A、 $\sqrt{3}$ B、 $\sqrt{3}$ +1 C、 $\sqrt{3}$ -1 D、 $\frac{\sqrt{3}}{3}$

查看试题解析
12. 如图，正方形ABCD中，对角线AC，BD交于点O，点M，N分别为OB，OC的中点，则cos∠OMN的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析

二、填空题

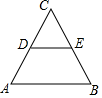
13. 计算: $\sqrt{2}$ cos45°=

查看试题解析
14. 抛物线y＝(x-2)²+3的顶点坐标是.

查看试题解析
15. 点A(-2,y₁),B(-1,y₂)都在反比例函数y=- $\frac{3}{x}$ 图象上,则y₁ y₂ (选填 “ ﹤” , “>”或” = ”)

查看试题解析
16. 如图，在△ABC中，D，E分别是AC，BC边上的中点，则三角形CDE的面积与四边形ABED的面积比等于

查看试题解析
17. 在正方形网格中，△ABC的位置如图所示，则sinB的值为

查看试题解析
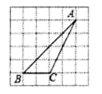18. 如图，四边形ABCD中，AB∥CD，∠B=90°，AB=1，CD=2，BC=3，点P为BC边上一动点，若△PAB与△PCD是相似三角形，则BP的长为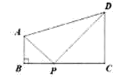

查看试题解析

三、解答题

19. 计算:
( $\frac{1}{2}$ )^-1 - $\sqrt{2}$ cos45° -(2020+π)⁰+3tan30°

查看试题解析
20. 已知正比例函数y=-3x与反比例函数y= $\frac{m - 5}{x}$ 交于点P(-1,n),求反比例函数的表达式

查看试题解析
21. 如图，在锐角三角形ABC中，AB=4，BC= $3 \sqrt{3}$ ，∠B=60°，求△ABC的面积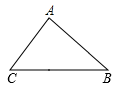

查看试题解析
22. 如图，在△ABC中，D为BC边上的一点，且∠CAD=∠B，CD=4，BD=2，求AC的长

查看试题解析
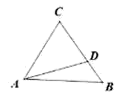23. 已知抛物线y=2x²-12x+13

(1)、当x为何值时,y有最小值,最小值是多少?

(2)、当x为何值时,y随x的增大而减小

(3)、将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出新抛物线的表达式

查看试题解析
24. 如图，在▱ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE= $\frac{1}{2}$ CD

(1)、求证：△ABF∽△CEB

(2)、若△DEF的面积为2，求△CEB的面积

查看试题解析
25. 某校有一露天舞台，纵断面如图所示，AC垂直于地面，AB表示楼梯，AE为舞台面，楼梯的坡角∠ABC=45°，坡长AB=2m，为保障安全，学校决定对该楼梯进行改造，降低坡度，拟修新楼梯AD，使∠ADC=30°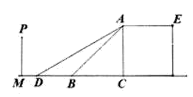

(1)、求舞台的高AC(结果保留根号)

(2)、楼梯口B左侧正前方距离舞台底部C点3m处的文化墙PM是否要拆除?请说明理由.

查看试题解析
26. 如图，已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，抛物线与x轴的另一交点为B．

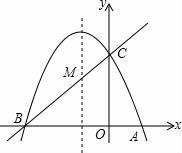(1)、若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；

(2)、设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．

查看试题解析