广西壮族自治区贵港市覃塘区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列各点不在反比例函数 的图象上的是( )A、 B、 C、 D、2. 在一幅比例尺为1:500000的地图上,若量得甲、乙两地的距离是25cm,则甲、乙两地实际距离为( )A、125km B、12.5km C、1.25km D、1250km3. 已知 ,且相似比为 ,若 ,则 的长是( )A、 B、 C、 D、4. 若用配方法解一元二次方程 ,则原方程可变形为( )A、 B、 C、 D、5. 已知一堤坝的坡度 ,堤坝的高度为 米,则堤坝的斜坡长为 ( )A、 米 B、 米 C、 米 D、 米6. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是 ( )A、 且 B、 且 C、 且 D、7. 计算 的结果是 ( )A、 B、 C、 D、8. 已知 一元二次方程 的两个实数根,且 ,则 的值为( )A、 或 B、 C、 D、9. 已知a,b,c是△ABC三条边的长,那么方程cx2+(a+b)x+ =0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定10. 如图,在 中,点 分别在 边上,且 ,若S四边形BCED ,则 的值为( )
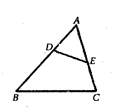 A、 B、 C、 D、11. 如图, 函数 与 的图象相交于点两点 ,则不等式 的解集为( )
A、 B、 C、 D、11. 如图, 函数 与 的图象相交于点两点 ,则不等式 的解集为( )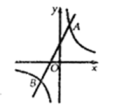 A、 B、 或 C、 D、 或12. 如图,在正方形 中, 是 边的中点,将 沿 折叠,使点 落在点 处, 的延长线与 边交于点 .下列四个结论:① ;② ;③ ;④ S正方形ABCD , 其中正确结论的个数为( )
A、 B、 或 C、 D、 或12. 如图,在正方形 中, 是 边的中点,将 沿 折叠,使点 落在点 处, 的延长线与 边交于点 .下列四个结论:① ;② ;③ ;④ S正方形ABCD , 其中正确结论的个数为( ) A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
13. 若 ,则 的值是 .14. 一组数据2,2,3,4,4的方差是.15. 如图,渔船在 处看到灯塔 在北偏东 方向上,渔船向正东方向航行了 到达 处,在 处看到灯塔 在正北方向上,则 处与灯塔 的距离是 .
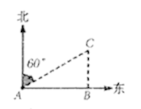 16. 已知 两直角边的长分别是方程 的两个实数根,且 的最小角为 ,则 的值是 .17. 如图,在平行四边形 中,点 在 边上,且 ,若 ,则 的长为 .
16. 已知 两直角边的长分别是方程 的两个实数根,且 的最小角为 ,则 的值是 .17. 如图,在平行四边形 中,点 在 边上,且 ,若 ,则 的长为 .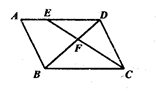 18. 如图,已知 中, , 顶点 分别在反比例函数 与 的图象上,则 的值为 .
18. 如图,已知 中, , 顶点 分别在反比例函数 与 的图象上,则 的值为 .
三、解答题
-
19.(1)、计算:
;
(2)、解方程:.
20. 如图,在平面直角坐标系 中, 的顶点为 .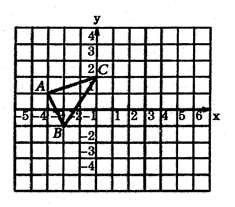 (1)、在 轴的右侧,画出 的位似图形 ,使位似中心为原点 ,位似比为(2)、写出 两点的坐标.21. 如图,在 中, 是斜边 的中线, 交 边于点 .
(1)、在 轴的右侧,画出 的位似图形 ,使位似中心为原点 ,位似比为(2)、写出 两点的坐标.21. 如图,在 中, 是斜边 的中线, 交 边于点 . (1)、求证: ;(2)、若 ,求 的长.22. 某市为了了解初中学校“高效课堂”的有效程度,并就初中生在课堂上是否具有“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”等学习行为进行评价.为此,该市教研部门开展了一次抽样调查, 并将调查结果绘制成尚不完整的条形统计图和扇形统计图(如图所示),请根据图中信息解答下列问题:
(1)、求证: ;(2)、若 ,求 的长.22. 某市为了了解初中学校“高效课堂”的有效程度,并就初中生在课堂上是否具有“主动质疑”、“独立思考”、“专注听讲”、“讲解题目”等学习行为进行评价.为此,该市教研部门开展了一次抽样调查, 并将调查结果绘制成尚不完整的条形统计图和扇形统计图(如图所示),请根据图中信息解答下列问题: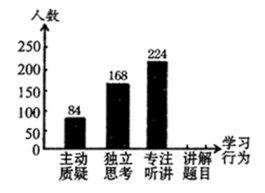 (1)、这次抽样调查的样本容量为.(2)、在扇形统计图中,“主动质疑”对应的圆心角为度;(3)、请补充完整条形统计图;
(1)、这次抽样调查的样本容量为.(2)、在扇形统计图中,“主动质疑”对应的圆心角为度;(3)、请补充完整条形统计图;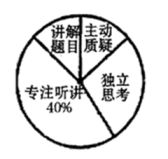 (4)、若该市初中学生共有 万人,在课堂上具有“独立思考”行为的学生约有多少人?23. 两栋居民楼之间的距离 ,楼 和 均为10层,每层楼高为 .上午某时刻,太阳光线 与水平面的夹角为30°,此刻楼 的影子会遮挡到楼 的第几层?(参考数据: , )
(4)、若该市初中学生共有 万人,在课堂上具有“独立思考”行为的学生约有多少人?23. 两栋居民楼之间的距离 ,楼 和 均为10层,每层楼高为 .上午某时刻,太阳光线 与水平面的夹角为30°,此刻楼 的影子会遮挡到楼 的第几层?(参考数据: , )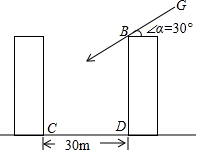 24. 为了满足师生的阅读需求,某校图书馆藏书总量由2017年 万册增加到2019年 万册.(1)、求该校图书馆这两年藏书总量的年均增长率;(2)、经统计知:在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书总量的年均增长率,2019年中外古典名著册数占藏书总量的 ,而在2017年中外古典名著册数仅占当年藏书总量的 ,请求出 的值.25. 如图,在平面直角坐标系 中,菱形 的对角线 经过原点 ,与 交于点 轴于点 ,点的坐标 为反比例函数 的图象恰好经过 两点.
24. 为了满足师生的阅读需求,某校图书馆藏书总量由2017年 万册增加到2019年 万册.(1)、求该校图书馆这两年藏书总量的年均增长率;(2)、经统计知:在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书总量的年均增长率,2019年中外古典名著册数占藏书总量的 ,而在2017年中外古典名著册数仅占当年藏书总量的 ,请求出 的值.25. 如图,在平面直角坐标系 中,菱形 的对角线 经过原点 ,与 交于点 轴于点 ,点的坐标 为反比例函数 的图象恰好经过 两点.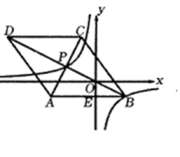 (1)、求 的值及 所在直线的表达式;(2)、求证: .(3)、求 的值.26. 把一副三角板按如图1所示放置,其中点 在 边上, ,斜边 .将三角板 绕点 顺时针旋转,记旋转角为 .
(1)、求 的值及 所在直线的表达式;(2)、求证: .(3)、求 的值.26. 把一副三角板按如图1所示放置,其中点 在 边上, ,斜边 .将三角板 绕点 顺时针旋转,记旋转角为 .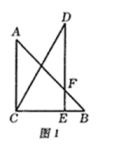
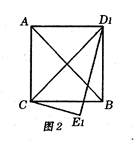
 (1)、在图1中,设 与 的交点为 ,则线段AF的长为;(2)、当 时,三角板 旋转到 ,的位置(如图2所示),连接 ,请判断四边形 的形状,并证明你的结论;(3)、当三角板 旋转到 的位置(如图3所示)时,此时点 恰好在 的延长线上.①求旋转角 的度数;②求线段 的长.
(1)、在图1中,设 与 的交点为 ,则线段AF的长为;(2)、当 时,三角板 旋转到 ,的位置(如图2所示),连接 ,请判断四边形 的形状,并证明你的结论;(3)、当三角板 旋转到 的位置(如图3所示)时,此时点 恰好在 的延长线上.①求旋转角 的度数;②求线段 的长.