辽宁省抚顺市顺城区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 下列各数与-6相等的( )A、|-6| B、-|-6| C、-32 D、-(-6)2. 有下列四个算式:①(﹣5)+(+3)=﹣8;②﹣(﹣2)3=6;③(+ )+(- )= ;④-3÷(- )=9.其中,正确的有( )A、0个 B、1个 C、2个 D、3个3. 如图是某会展中心展出的一只紫砂壶,你认为是从上面看到的效果图是( )
 A、
A、 B、
B、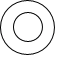 C、
C、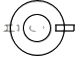 D、
D、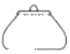 4. 如果a表示有理数,那么下列说法中正确的是( )A、+a和一(-a)互为相反数 B、+a和-a一定不相等 C、-a一定是负数 D、-(+a)和+(-a)一定相等5. a,b是有理数,它们在数轴上的对应点的位置如所示:把a,﹣a,b,﹣b按照由小到大的顺序排列是( )
4. 如果a表示有理数,那么下列说法中正确的是( )A、+a和一(-a)互为相反数 B、+a和-a一定不相等 C、-a一定是负数 D、-(+a)和+(-a)一定相等5. a,b是有理数,它们在数轴上的对应点的位置如所示:把a,﹣a,b,﹣b按照由小到大的顺序排列是( ) A、﹣b<﹣a<b<a B、﹣a<b<﹣b<a C、﹣a<﹣b<b<a D、b<﹣a<-b<a6. 下列图形不是正方体的表面展开图的是( )A、
A、﹣b<﹣a<b<a B、﹣a<b<﹣b<a C、﹣a<﹣b<b<a D、b<﹣a<-b<a6. 下列图形不是正方体的表面展开图的是( )A、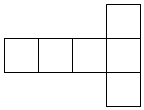 B、
B、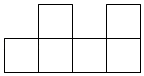 C、
C、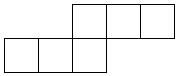 D、
D、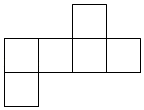 7. 下列说法正确的是( )A、一点确定一条直线 B、两条射线组成的图形叫角 C、两点之间线段最短 D、若AB=BC,则B为AC的中点8. 如图,时针与分针的夹角是( )
7. 下列说法正确的是( )A、一点确定一条直线 B、两条射线组成的图形叫角 C、两点之间线段最短 D、若AB=BC,则B为AC的中点8. 如图,时针与分针的夹角是( ) A、75° B、65° C、55° D、45°9. 如图,OC在∠AOB的内部,∠BOC:∠AOC=1:2.∠AOB=63°,则∠AOC=( )
A、75° B、65° C、55° D、45°9. 如图,OC在∠AOB的内部,∠BOC:∠AOC=1:2.∠AOB=63°,则∠AOC=( )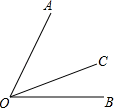 A、52° B、42° C、39° D、21°10. 找出以下图形变化的规律,则第(100)个图形中黑色正方形的数量是( )
A、52° B、42° C、39° D、21°10. 找出以下图形变化的规律,则第(100)个图形中黑色正方形的数量是( ) A、150 B、151 C、152 D、153
A、150 B、151 C、152 D、153二、填空题
-
11. 过度包装既浪费资源又污染环境.据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量.把数据3120000用科学记数法表示为 .
12. 若a、b是互为倒数,则2ab﹣5= .13. 已知∠α+∠β=90°,且∠α=36°40′,则∠β= .14. 已知2x+4与3x﹣2互为相反数,则x=.15. 点A、B、C是同一直线上的三个点,若AB=8cm,BC=3cm,则AC= cm.16. 如图,∠AOC=150°,则射线OA的方向是 .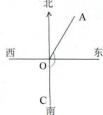 17. 某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.如表记录了5个参赛者的得分情况.在此次竞赛中,有一位参赛者答对15道题,答错5道题,则他的得分是 .
17. 某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.如表记录了5个参赛者的得分情况.在此次竞赛中,有一位参赛者答对15道题,答错5道题,则他的得分是 .参赛
答对题数
答错题数
得分
A
19
1
112
B
18
2
104
C
17
3
96
D
12
8
56
E
10
10
40
18. 已知整数a1 , a2 , a3 , a4 , …满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2020的值为 .三、解答题
-
19. 计算:(1)、7+(﹣28)﹣(﹣9)(2)、﹣32+(﹣12)×|﹣ |﹣6÷(﹣1)(3)、﹣14+ ×[2×(﹣6)﹣(﹣4)2]20. 先化简,再求值:(1)、2(x2+2x﹣2)﹣(x2﹣2x﹣1),其中x=﹣ .(2)、(2x2﹣2y2)﹣3(x2y2+x2)+3(x2y2+y2),其中x=﹣1,y=2.21. 解方程:(1)、9(x-3)2-49=0(2)、2x2-3x-2=2x+122. 如图,已知直线 和直线外三点 ,按下列要求画图:
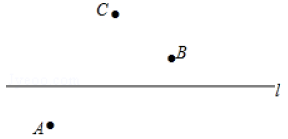
①画射线 ;
②连接 ;
③延长 至 ,使得 ;
④在直线 上确定点 ,使得 最小.
23. 如图,∠AOC是直角,OD平分∠AOC,∠BOC=60° 求: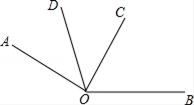 (1)、∠AOD的度数;(2)、∠AOB的度数;(3)、∠DOB的度数.24. 如图,图①所示是一个长为2m,宽为2n的长方形,用剪刀均分成四个小长方形,然后按图②的方式拼成一个大正方形.
(1)、∠AOD的度数;(2)、∠AOB的度数;(3)、∠DOB的度数.24. 如图,图①所示是一个长为2m,宽为2n的长方形,用剪刀均分成四个小长方形,然后按图②的方式拼成一个大正方形.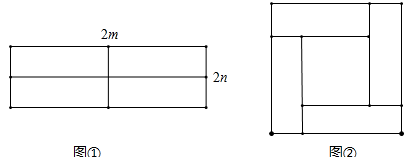 (1)、图②中的大正方形的边长等于 , 图②中的小正方形的边长等于;(2)、图②中的大正方形的面积等于 , 图②中的小正方形的面积等于;图①中每个小长方形的面积是;(3)、观察图②,你能写出(m+n)2 , (m﹣n)2 , mn这三个代数式间的等量关系吗? .25. 将一副三角板放在同一平面内,使直角顶点重合于点O
(1)、图②中的大正方形的边长等于 , 图②中的小正方形的边长等于;(2)、图②中的大正方形的面积等于 , 图②中的小正方形的面积等于;图①中每个小长方形的面积是;(3)、观察图②,你能写出(m+n)2 , (m﹣n)2 , mn这三个代数式间的等量关系吗? .25. 将一副三角板放在同一平面内,使直角顶点重合于点O
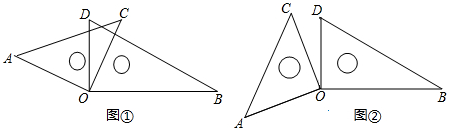 (1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.26. 某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生(其中甲校学生多于乙校学生,且甲校学生不足90名),现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
(1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.26. 某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生(其中甲校学生多于乙校学生,且甲校学生不足90名),现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
如果两所学校单独购买服装,一共应付5000元。
(1)、甲、乙两校各有多少名学生准备参加汇演?(2)、如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)、如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱。27. 在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.(1)、甲、乙两队合作多少天?(2)、甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?28. 为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现,甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球,乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少?(2)、若城区四校联合购买100套队服和 个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;(3)、在(2)的条件下,若 ,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?29. 已知线段AB=30cm (1)、如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?(2)、如图1,几秒后,点P、Q两点相距10cm?(3)、如图2,AO=4cm,PO=2cm,当点P在AB的上方,且∠POB=60°时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.
(1)、如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?(2)、如图1,几秒后,点P、Q两点相距10cm?(3)、如图2,AO=4cm,PO=2cm,当点P在AB的上方,且∠POB=60°时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.