湖北省十堰市丹江口市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 四个有理数 、1、0、 ,其中最小的是( )A、0 B、1 C、 D、2. 习近平同志在十九大报告中指出:农业农村农民问题是关系到国计民生的根本性问题,我国现有农村人口约为589 730 000人,将589 730 000用科学记数法表示为( )A、589 73×104 B、589.73×106 C、5.8973×108 D、0.58973×1083. 下列运算正确的是( )A、 B、 C、 D、4. 若x=1是关于x的方程2x+a=1的解,则a的值为( )A、 B、1 C、3 D、5. 在数轴上,实数a,b对应的点的位置如图所示,且这两个点到原点的距离相等,下列结论中,正确的是( )
 A、 B、 C、 D、6. 有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中 , , , 中的( )位置接正方形.
A、 B、 C、 D、6. 有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形折叠后能成为一个封闭的正方体盒子,你不能选择图中 , , , 中的( )位置接正方形.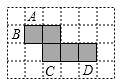 A、 B、 C、 D、7. 若 满足 ,则 等于( )A、8 B、6 C、 D、8. 如图,一副三角尺按不同的位置摆放,摆放位置中 的图形的个数是( )
A、 B、 C、 D、7. 若 满足 ,则 等于( )A、8 B、6 C、 D、8. 如图,一副三角尺按不同的位置摆放,摆放位置中 的图形的个数是( )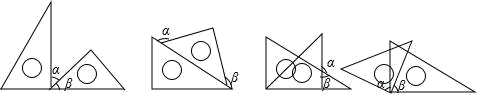 A、 B、 C、 D、9. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、10. 一列火车长 米,以每秒 米的速度通过一个长为 米的隧道,用式子表示它刚好从开始进隧道口到全部通过隧道所需的时间为( )秒A、 B、 C、 D、
A、 B、 C、 D、9. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、10. 一列火车长 米,以每秒 米的速度通过一个长为 米的隧道,用式子表示它刚好从开始进隧道口到全部通过隧道所需的时间为( )秒A、 B、 C、 D、二、填空题
-
11. 某市2020年元旦的最低气温为 ,最高气温为 ,这一天的最高温度比最低温度高12. 单项式 的系数是 , 次数是.13. 若 ,则 的余角是.14. 如图所示的运算程序中,若开始输入的 值为12,我们发现第1次输出的结果为6,第2次输出的结果为3,…,第2020次输出的结果为.
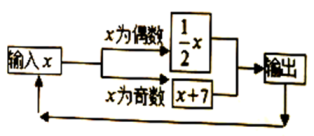
三、解答题
-
15. 计算题:(1)、(2)、16. 解方程:(1)、(2)、17. 先化简,再求值: ,其中 .18. 作图题:如图,在平面内有不共线的3个点, , , .
 (1)、①作射线 ,在 延长线上取一点 ,使 ;
(1)、①作射线 ,在 延长线上取一点 ,使 ;②作线段 并延长 到点 ,使 ;
③连接 , ;
(2)、度量线段 和 的长度,直接写出二者之间的数量关系,观察 和 的位置是(填“平行”或“相交”)关系;(3)、作 的中点 ,连接 ,猜想 (填“ ”,“ ”或“ ”)19. 一个长方形一边长为 ,另一边长为 .(1)、用含有 的式子表示这个长方形的周长;(2)、若 满足 ,求它的周长.20. 在作解方程练习时,学习卷中有一个方程“ ”中的 没印清晰,小聪问老师,老师只是说:“ 是个有理数,该方程的解与方程 的解相同.”小聪很快补上了这个常数,聪明的你能补上这个常数吗?21. 对于任意四个有理数 ,我们规定: ,例如: ,根据上述规定解决下列问题:(1)、计算 ;(2)、若有理数对 ,求 的值.22. 为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.下表是小明家1至4月份水量和缴纳水费情况,根据表格提供的数据,回答:月份
一
二
三
四
用水量(吨)
7
9
12
15
水费(元)
14
18
26
35
(1)、规定用量内的收费标准是元/吨,超过部分的收费标准是元/吨;(2)、问该市每户每月用水规定量是多少吨?(3)、若小明家六月份应缴水费50元,则六月份他们家的用水量是多少吨?23. 已知数轴上,点 和点 分别位于原点 两侧,点 对应的数为 ,点 对应的数为 ,且 .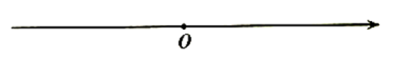 (1)、若 ,则 的值为.(2)、若 ,求 的值;(3)、点 为数轴上一点,对应的数为 ,若 点在原点的左侧, 为 的中点, ,请画出图形并求出满足条件的 的值.24. 如图1,已知 , 在 内, 在 内, .
(1)、若 ,则 的值为.(2)、若 ,求 的值;(3)、点 为数轴上一点,对应的数为 ,若 点在原点的左侧, 为 的中点, ,请画出图形并求出满足条件的 的值.24. 如图1,已知 , 在 内, 在 内, .
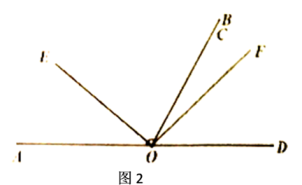 (1)、 从图1中的位置绕点 逆时针旋转到 与 重合时,如图2, ;(2)、若图1中的 平分 ,则 从图1中的位置绕点 逆时针旋转到 与 重合时,旋转了多少度?(3)、 从图2中的位置绕点 逆时针旋转 ,试问:在旋转过程中 的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.
(1)、 从图1中的位置绕点 逆时针旋转到 与 重合时,如图2, ;(2)、若图1中的 平分 ,则 从图1中的位置绕点 逆时针旋转到 与 重合时,旋转了多少度?(3)、 从图2中的位置绕点 逆时针旋转 ,试问:在旋转过程中 的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.