浙江省宁波市奉化区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-26 类型:期末考试
一、单选题
-
1. 数0是( )A、最小整数 B、最小正数 C、最小自然数 D、最小有理数2. 下列图形中表示北偏东60°的射线是( )A、
 B、
B、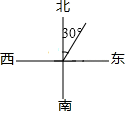 C、
C、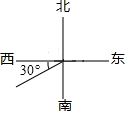 D、
D、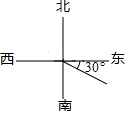 3. 2019年10月1日,庆视中华人民共和国成立70周年阅兵在天安门广场隆重举行.此次阅兵是近年规模最大的一次,共编59个方(梯)队和联合军乐团,总规模约15000人,则15000用科学记数法可以表示为( )A、 B、 C、 D、4. 把一条弯曲的公路改成直道,可以缩短路程,这其中蕴含的数学道理是( )A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、两点之间直线最短5. 已知 ,则 的余角是( )A、 B、 C、 D、6. 把方程 的分母化为整数,正确的是( )A、 B、 C、 D、7. 在 中,用数字4替换其中的一个非0数字后,使所得的数最大,则被替换的数字是( )A、1 B、3 C、6 D、88. 张老师有一批屯册准备分给苦干个小朋友,如果每3人分到一本,那么还剩2本;如果每2人分到一本,那么还有9人没有分到.设小朋友的人数为 人,则可以列出方程是( )A、 B、 C、 D、9. 在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内水面的形状不可能是( )A、
3. 2019年10月1日,庆视中华人民共和国成立70周年阅兵在天安门广场隆重举行.此次阅兵是近年规模最大的一次,共编59个方(梯)队和联合军乐团,总规模约15000人,则15000用科学记数法可以表示为( )A、 B、 C、 D、4. 把一条弯曲的公路改成直道,可以缩短路程,这其中蕴含的数学道理是( )A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、两点之间直线最短5. 已知 ,则 的余角是( )A、 B、 C、 D、6. 把方程 的分母化为整数,正确的是( )A、 B、 C、 D、7. 在 中,用数字4替换其中的一个非0数字后,使所得的数最大,则被替换的数字是( )A、1 B、3 C、6 D、88. 张老师有一批屯册准备分给苦干个小朋友,如果每3人分到一本,那么还剩2本;如果每2人分到一本,那么还有9人没有分到.设小朋友的人数为 人,则可以列出方程是( )A、 B、 C、 D、9. 在一个无盖的正方体玻璃容器内装了一些水,把容器按不同方式倾斜一点,容器内水面的形状不可能是( )A、 B、
B、 C、
C、 D、
D、 10. 以下结论:①单项式 的系数是 ,次数是4;②化简代数式: ;③在 ,0, , , , 中,整式有4个;④ 的平方根可以表示为: .正确的有( )个.A、0 B、1 C、2 D、311. 如图,点 、 、 顺次在直线 上,点 是线段 的中点,点 是线段 的中点.若想求出 的长度,则只需条件( )
10. 以下结论:①单项式 的系数是 ,次数是4;②化简代数式: ;③在 ,0, , , , 中,整式有4个;④ 的平方根可以表示为: .正确的有( )个.A、0 B、1 C、2 D、311. 如图,点 、 、 顺次在直线 上,点 是线段 的中点,点 是线段 的中点.若想求出 的长度,则只需条件( )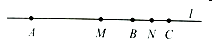 A、 B、 C、 D、12. 任意大于1的正整数 的三次幂均可“分裂”成 个连续奇数的和.如: , , .……,若 的“分裂数”中有一个是119,则 ( )A、10 B、11 C、12 D、13
A、 B、 C、 D、12. 任意大于1的正整数 的三次幂均可“分裂”成 个连续奇数的和.如: , , .……,若 的“分裂数”中有一个是119,则 ( )A、10 B、11 C、12 D、13二、填空题
-
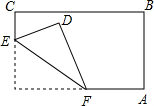
13. 近似数3.60×105精确到位14. 绝对值小于 的整数有个.15. .16. 拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF,如果 ,则 .
 17. 若 是关于 的三次二项式,则 .18. 如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形 的周长为 ,阴影部分的周长为 那么以下四个正方形中号正方形的边长可以直接用 、 表示,结果为.
17. 若 是关于 的三次二项式,则 .18. 如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重叠也无空隙.已知矩形 的周长为 ,阴影部分的周长为 那么以下四个正方形中号正方形的边长可以直接用 、 表示,结果为.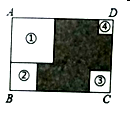
三、解答题
-
19. 在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“ ”连接:
, , ,0, ,
 20. 解方程:(1)、(2)、21. 根据下列语句,画出图形.
20. 解方程:(1)、(2)、21. 根据下列语句,画出图形.如图,已知平面内有四个点 、 、 、 ,共中任意三点都不在同一直线上.
①画直线 ;
②连接 、 ,相交于点 ;
③画射线 、 ,交于点 ;
④过点 作 所在直线的垂线段,垂足为点
 22. 已知点 是直线 上一点, 是直角, 平分 .
22. 已知点 是直线 上一点, 是直角, 平分 .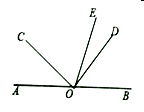 (1)、如图,若 ,求 的度数;(2)、在图中,若 ,则 (用含 的代数式表示)23. 设 ,(1)、求 ;(2)、已知 , 求 的值.24. 生态公园计划在园内的坡地上造一片有 、 两种树的混合林,需要购买这两种树苗2000棵,种植 、 两种树苗的相关信息如下表:
(1)、如图,若 ,求 的度数;(2)、在图中,若 ,则 (用含 的代数式表示)23. 设 ,(1)、求 ;(2)、已知 , 求 的值.24. 生态公园计划在园内的坡地上造一片有 、 两种树的混合林,需要购买这两种树苗2000棵,种植 、 两种树苗的相关信息如下表:品名
单价(元/棵)
栽树劳务费(元/棵)
成活率
25
3
30
4
设购买 种树苗 棵,解答下列问题:
(1)、购买的 种树苗的数量为棵(含 的代数式表示);(2)、请用含 的代数式表示造这片林的总费用;(3)、假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?25. 如图,数轴上有 、 、 、 四个点,分别对应 , , , 四个数,其中 , , 与 互为相反数, (1)、求 , 的值;(2)、若线段 以每秒3个单位的速度,向右匀速运动,当 时,点 与点 重合,当 时,点 与点 重合;(3)、若线段 以每秒3个单位的速度向右匀速运动的同时,线段 以每秒2个单位的速度向左匀速运动,则线段 从开始运动到完全通过 所需时间多少秒?(4)、在(3)的条件下,当点 运动到点 的右侧时,是否存在时间 ,使点 与点 的距离是点 与点 的距离的4倍?若存在,请求出 值,若不存在,请说明理由.
(1)、求 , 的值;(2)、若线段 以每秒3个单位的速度,向右匀速运动,当 时,点 与点 重合,当 时,点 与点 重合;(3)、若线段 以每秒3个单位的速度向右匀速运动的同时,线段 以每秒2个单位的速度向左匀速运动,则线段 从开始运动到完全通过 所需时间多少秒?(4)、在(3)的条件下,当点 运动到点 的右侧时,是否存在时间 ,使点 与点 的距离是点 与点 的距离的4倍?若存在,请求出 值,若不存在,请说明理由.