安徽省淮南市谢家集区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-02-24 类型：期中考试

进入出卷网下载

一、单选题

1. $- \sqrt{3}$ 的相反数是（）

A、 $\frac{\sqrt{3}}{3}$ B、- $\frac{\sqrt{3}}{3}$ C、 $\sqrt{3}$ D、 $- \sqrt{3}$

查看试题解析
2. 在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是（）

A、（5，﹣4） B、（﹣1，﹣6） C、（﹣3，10） D、（7，3）

查看试题解析
3. 如图，∠1＝∠2，则下列结论一定成立的是（）

A、AB∥CD B、AD∥BC C、∠B＝∠D D、∠3＝∠4

查看试题解析
4. 下列命题中，是真命题的是（）

A、若a⊥b ， b⊥c ，则a⊥c B、在坐标平面内P（﹣2，3）到x轴上的距离等于2 C、无限小数都是无理数 D、经过直线外一点，有且只有一条直线与这条直线平行

查看试题解析
5. 在平面直角坐标系中，点（﹣2，﹣a²﹣3）一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，已知a∥b，直角三角板的直角顶点在直线b上，若∠1=60°，则下列结论错误的是（）

A、∠2=60° B、∠3=60° C、∠4=120° D、∠5=40°

查看试题解析
7. 右边运算中错误的有（）：① $\sqrt{16}$ ＝4；② $\sqrt[3]{{(- 8)}^{2}} = 4$ ；③ $\sqrt{- 4^{2}} = - 4$ ；④ $\sqrt{{(- 4)}^{2}} = 4$ ；⑤± $\sqrt{4} = 4$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知点A（1，0），B（0，3），点P在x轴上，且三角形PAB的面积为3，则点P的坐标是（）

A、（﹣1，0） B、（3，0） C、（﹣1，0）或（3，0） D、（0，9）或（0，﹣3）

查看试题解析
9. 如图，小明从家到学校分别有①、②、③三条路可走：①为折线段ABCDEFG ， ②为折线段AIG ， ③为折线段AJHG ．三条路的长依次为a、b、c ，则（）

A、a＞b＞c B、a＝b＞c C、a＞c＞b D、a＝b＜c

查看试题解析
10. 在平面直角坐标系中，对于点P（x ， y），我们把点P'（﹣y+1，x+1）叫做点P伴随点已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂A₃ ， …，A_n ， …若点A₁的坐标为（2，4），点A₂₀₁₉的坐标为（）

A、（﹣3，3） B、（﹣2，﹣2） C、（3，﹣1） D、（2，4）

查看试题解析

二、填空题

11. 写出一个比﹣π大的负无理数：．

查看试题解析
12. 在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB，CD，并说出自己做法的依据．小琛、小萱、小冉三位同学的做法如下：
小琛说：“我的做法的依据是内错角相等，两直线平行．”
小萱做法的依据是．
小冉做法的依据是．

查看试题解析
13. P（m﹣1，2﹣m）在y轴上，则m＝．

查看试题解析
14. 若 $\sqrt{a + 2} + | b - 3 | = 0$ ，则a^b＝．

查看试题解析
15. 线段CD是由线段AB平移得到的，点A（﹣1，﹣4）的对应点为C（3，0），则点B（﹣3，1）的应点D的坐标为．

查看试题解析
16. 规定用符号[m]表示一个实数m的整数部分，例如[ $\frac{2}{3}$ ]＝0，[3.14]＝3．按此规定 $[- \sqrt{17} + 1]$ 的值为．

查看试题解析
17. 已知P（2+x ， 3x﹣2）到x轴的距离是到y轴的距离的2倍，则x的值为．

查看试题解析
18. 如图，三角形ABC中，∠ACB＝90°，AC＝3，BC＝4，AB＝5，P为直线AB上一动点，连PC，则线段PC的最小值是．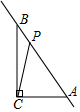

查看试题解析

三、解答题

19.

(1)、 $\sqrt[3]{8} + | 3 - \sqrt{3} | - \sqrt{25} + \sqrt{3}$

(2)、如果2a﹣1和3﹣a是一个正数的平方根，6a+b的立方根是﹣2，求2a+b的平方根．

查看试题解析
20. 如图，直线AB ， CD相交于点O ， ∠AOC＝60°，∠1∶∠2＝1∶2.

(1)、求∠2的度数；

(2)、若∠2与∠MOE互余，求∠MOB的度数．

查看试题解析
21. 请根据如图所示的对话内容回答下列问题．

(1)、求该魔方的棱长；

(2)、求该长方体纸盒的表面积．

查看试题解析
22. 如图

(1)、①如图1，AB∥CD ，则∠B、∠P、∠D之间的关系是；
②如图2，AB∥CD ，则∠A、∠E、∠C之间的关系是；

(2)、①将图1中BA绕B点逆时针旋转一定角度交CD于Q（如图3）．证明：∠BPD＝∠1+∠2+∠3
②将图2中AB绕点A顺时针旋转一定角度交CD于H（如图4）证明：∠E+∠C+∠CHA+∠A＝360°

(3)、利用（2）中的结论求图5中∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数．

查看试题解析