安徽省合肥市蜀山区2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-02-24 类型：期中考试

进入出卷网下载

一、单选题

1. 计算（ $\frac{1}{3}$ ）^﹣¹的结果为（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 不等式a＞0表示的意义是（）

A、a不是负数 B、a是负数 C、a是非负数 D、a是正数

查看试题解析
3. 下列计算中，正确是（）

A、（π﹣3.14）⁰＝1 B、（x﹣2）²＝x²﹣4 C、﹣a³•（﹣a）²＝a⁶ D、（﹣ $\frac{1}{2}$ x²y）³＝﹣ $\frac{1}{6}$ x⁶y³

查看试题解析
4. 将不等式组 ${\begin{array}{l} x - 1 > 0 \\ x - 3 \leq 0 \end{array}$ 的解集在数轴上表示出来正确是（）

A、 B、 C、 D、

查看试题解析
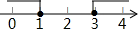5. 已知一个正方形的边长为a ，将该正方形的边长增加1，则得到的新正方形的面积为（）

A、a²+2a+1 B、a²﹣2a+1 C、a²+1 D、a+1

查看试题解析
6. 下列运算正确是（）

A、（x+3y）（x﹣3y）＝x²﹣3y² B、（x+3y）（x﹣3y）＝x²﹣9y² C、（﹣x+3y）（x﹣3y）＝﹣x²﹣9y² D、（﹣x﹣3y）（x+3y）＝x²﹣9y²

查看试题解析
7. 若x²+mxy+ $\frac{25}{4}$ y²是完全平方式，则常数m的值为（）

A、5 B、﹣5 C、±5 D、± $\frac{25}{2}$

查看试题解析
8. 若 $\sqrt[3]{x} + \sqrt[3]{y} =0$ ，则x和y的关系是（）．

A、x＝y＝0 B、x和y互为相反数 C、x和y相等 D、不能确定

查看试题解析
9. 若2x³﹣ax²﹣5x+5＝（2x²+ax﹣1）（x﹣b）+3，其中a ， b为整数，则ab的值为（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
10. 关于x的不等式组 ${\begin{array}{l} 3 x - 2 > 4 (x - 1) \\ x < a \end{array}$ 的解集为x＜2，那么a的取值范围为（）

A、a＝2 B、a＞2 C、a＜2 D、a≥2

查看试题解析

二、填空题

11. 科学记数法表示0.00000016为米．

查看试题解析
12. 填空：（2a+b）（）＝4a²+4ab+b² ．

查看试题解析
13. 某水果店花费760元购进一种水果40千克，在运输与销售过程中，有5%的水果正常损耗，为了避免亏本，售价至少应定为元/千克．

查看试题解析
14. 已知（a+b）²＝7，|ab|＝3，则 $\frac{1}{2}$ （a²+b²）﹣ab＝．

查看试题解析

三、解答题

15. 计算： $- \sqrt{9} + {(- \frac{1}{3})}^{- 1} \times {(\sqrt{3} - 1)}^{0}$ ．

查看试题解析
16. 解不等式组 ${\begin{array}{l} \frac{1}{2} (x - 1) ⩽ 1 \\ x - 3 < 3 x + 1 \end{array}$ 并将其解集在数轴上表示出来．

查看试题解析
17. 现有一个长方体木箱，底面是一个正方形，高为3m ，体积为4.32m³ ，求该木箱的底面周长．

查看试题解析
18. 化简：4a（4a+3）﹣（2a+1）（2a﹣1），若a满足a²+a＝7，求原代数式的值．

查看试题解析
19. 观察下列关于自然数的等式：
5²﹣9×2²＝﹣11…①

8²﹣9×3²＝﹣17…②

11²﹣9×4²＝﹣23…③

…

根据上述规律，解决下列问题：

(1)、完成第四个等式：14²﹣9×＝．

(2)、根据上面的规律写出你猜想的第n个等式（用含n的等式表示），并验证其符合题意性．

查看试题解析
20. 爱动脑筋的丽丽与娜娜在做数学小游戏，两人各报一个整式，丽丽报的整式A作被除式，娜娜报的整式B作除式，要求商式必须为﹣3xy（即A÷B＝﹣3xy）

(1)、若丽丽报的是x³y﹣6xy² ，则娜娜应报什么整式？

(2)、若娜娜也报x³y﹣6xy² ，则丽丽能报一个整式吗？若能，则是个什么整式？说说你的理由．

查看试题解析
21. 阅读：为了求1+2+2²+2³+…+2¹⁰⁰⁰的值，
令S＝1+2+2²+2³+…+2¹⁰⁰⁰ ，

则2S＝2+2²+2³+2⁴+…+2¹⁰⁰¹ ，

因此2S﹣S＝，

所以1+2+2²+2³+…+2¹⁰⁰⁰＝．

应用：仿照以上推理计算出1+6+6²+6³+…+6²⁰¹⁹的值．

查看试题解析
22. 为了扶贫户学生好读书，读好书，某实验学校校友会在今年开学初，到新华书店采购文学名著和自然科学两类图书．经了解，购买30本文学名著和50本自然科学书共需2350元，20本文学名著比20本自然科学书贵500元．（注：所采购的文学名著价格都一样，所采购的自然科学书价格都一样）

(1)、求每本文学名著和自然科学书的单价．

(2)、若该校校友会要求购买自然科学书比文学名著多30本，自然科学书和文学名著的总数不低于80本，总费用不超过2400元，请求出所有符合条件的购书方案．

查看试题解析
23. 当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1可得等式：（a+2b）（a+b）＝a²+3ab+2b² ．

(1)、由图2可得等式：．

(2)、利用（1）中所得到的结论，解决下面的问题：
已知a+b+c＝13，ab+bc+ac＝52，求a²+b²+c²的值．

(3)、利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：（3a+b）（a+3b）＝3a²+10ab+3b² ．

查看试题解析