安徽省滁州市明光市2017-2018学年七年级下学期数学期中考试试卷
试卷更新日期:2020-02-24 类型:期中考试
一、单选题
-
1. 的算术平方根是( )A、9 B、±9 C、±3 D、32. 在实数 ,- ,π, ,2.3010010001…,4- 中,无理数的个数是( )A、5 B、4 C、3 D、23. 不等式组 的解集在数轴上表示为( )
A、 B、
B、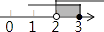 C、
C、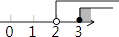 D、
D、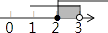 4. 下列计算正确是( )A、 B、 C、 D、5. 一个长方体的长为0.02米,宽为0.016米,则这个长方形的面积用科学记数法表示为( )A、 B、 C、 D、6. 已知 +(b+ )2=0,则a2016b2017的值是( )A、2 B、 C、 D、7. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
4. 下列计算正确是( )A、 B、 C、 D、5. 一个长方体的长为0.02米,宽为0.016米,则这个长方形的面积用科学记数法表示为( )A、 B、 C、 D、6. 已知 +(b+ )2=0,则a2016b2017的值是( )A、2 B、 C、 D、7. 图(1)是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )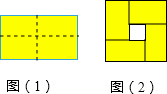 A、2mn B、(m+n)2 C、(m-n)2 D、m2-n28. 下列各式中不能用公式法分解因式的是A、x2-6x+9 B、-x2+y2 C、x2+2x+4 D、-x2+2xy-y29. 若a>0,且ax=3,ay=2,则a2x-y的值为( )A、3 B、4 C、 D、710. 某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
A、2mn B、(m+n)2 C、(m-n)2 D、m2-n28. 下列各式中不能用公式法分解因式的是A、x2-6x+9 B、-x2+y2 C、x2+2x+4 D、-x2+2xy-y29. 若a>0,且ax=3,ay=2,则a2x-y的值为( )A、3 B、4 C、 D、710. 某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )包场计费:包场每场每小时50元,每人须另付入场费5元
人数计费:每人打球2小时20元,接着续打球每人每小时6元
A、9 B、8 C、7 D、6二、填空题
-
11. 已知n为正整数,且n< <n+1,则 的值是 .12. 若多项式x2+mx+4在整数范围内可分解因式,则m的值是 .13. 已知不等式组 无解,则a的取值范围是 .14. 观察下列等式:
;
;
;
…………
则第 ( 是正整数)个等式为.
三、解答题
-
15. 计算:(1)、 - +(π-3)0+|1- |;(2)、(-4x2y)2•(-xy2)÷(-2x5y3).16. 因式分解:(1)、-2ax2+8ay2;(2)、4m2-n2+6n-9.17. 解不等式(3x+4)(3x-4)-x(x-4)>8(x+1)2 , 并把它的解集在数轴上表示出来.
 18. 如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
18. 如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.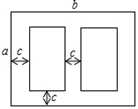 (1)、用代数式表示这两个篮球场的占地面积.(2)、当a=30,b=40,c=3时,计算出一个篮球场的面积.19. 对于任意实数a、b、c、d,我们规定 =ad-bc,若-8< <4,求整数x的值.20. 已知a+b=3,ab=-2,求下列各式的值.(1)、a2+b2;(2)、a-b.21. 现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
(1)、用代数式表示这两个篮球场的占地面积.(2)、当a=30,b=40,c=3时,计算出一个篮球场的面积.19. 对于任意实数a、b、c、d,我们规定 =ad-bc,若-8< <4,求整数x的值.20. 已知a+b=3,ab=-2,求下列各式的值.(1)、a2+b2;(2)、a-b.21. 现有若干张如图1所示的正方形纸片A,B和长方形纸片C.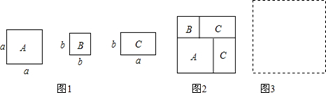 (1)、小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式: ;(2)、小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 ,并请你在图3位置画出拼成的长方形;(3)、根据拼图经验,请将多项式a2+5ab+4b2分解因式.22. 某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
(1)、小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式: ;(2)、小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 ,并请你在图3位置画出拼成的长方形;(3)、根据拼图经验,请将多项式a2+5ab+4b2分解因式.22. 某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.A
B
载客量(人/辆)
40
20
租金(元/辆)
200
150
(1)、若要保证租金费用不超过980元,请问该学校有哪几种租车方案?(2)、在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?23.(1)、填空:;
;
;
(2)、猜想:(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)= (其中n为正整数,且n≥2);
(3)、利用(2)猜想的结论计算:①29+28+27+…+22+2+1
②210-29+28-…-23+22-2.