安徽省芜湖市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-02-24 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{9}$ 的结果中（）

A、9 B、-9 C、3 D、-3

查看试题解析
2. 式子 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值是（）

A、 $x < - 2$ B、 $x \geq - 2$ C、 $x \leq - 2$ D、 $x > - 2$

查看试题解析
3. 在以线段a，b，c的长三边的三角形中，不能构成直角三角形的是（）

A、a=4,b=5,c=6 B、a:b:c=5:12:13 C、 $a = \sqrt{2}$ ， $b = \sqrt{3}$ ， $c = \sqrt{5}$ D、a=4,b=5,c=3

查看试题解析
4. 下列各式中，属于最简二次根式的是（）

A、 $\sqrt{16}$ B、 $\sqrt{0.5}$ C、 $\sqrt{7}$ D、 $\sqrt{12}$

查看试题解析
5. 如图，在矩形ABCD中，AB与BC的长度比为3：4，若该矩形的周长为28，则BD的长为（）

A、5 B、6 C、8 D、10

查看试题解析
6. $\sqrt{14} - 1$ 整数部分是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，在菱形ABCD中，AB=3，∠ABC=60°，则对角线BD的长是（）

A、 $6 \sqrt{3}$ B、 $3 \sqrt{3}$ C、6 D、3

查看试题解析
8. 已知一个直角三角形斜边为20，一条直角边长为16，那么它的面积是（）

A、160 B、48 C、60 D、96

查看试题解析
9. 在四边形ABCD中：①AB∥CD②AD∥BC③AB=CD④AD=BC，从以上选择两个条件使四边形ABCD为平行四边形的选法共有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
10. 如图，在矩形ABCD中，DE⊥AC于E，∠EDC：∠EDA=1：3 ，且AC=12，则DE的长度是（）

A、3 B、6 C、 $2 \sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析

二、解答题

11. 计算： $\sqrt{8} \div \sqrt{\frac{1}{2}}$ =。

查看试题解析
12. 计算： $\sqrt{12} \times \sqrt{\frac{2}{3}} + （ \sqrt{2} - 1 ）^{2}$ .

查看试题解析
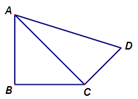
13. 已知 $x = \frac{1}{\sqrt{2} + 1}$ ， $y = \frac{1}{\sqrt{2} - 1}$ ，分别求下列代数式的值；

(1)、 $x^{2} + y^{2}$ ；

(2)、 $\frac{y}{x} + \frac{x}{y}$ .

查看试题解析
14. 如图，在四边形ABCD中，AB=BC=3，CD= $\sqrt{7}$ ，DA=5，∠B=90°，求∠BCD的度数

查看试题解析
15. 如图，在平行四边形ABCD中，直线GH分别与边CB，AD的延长线相交于点E，F，且G，H分别在AB，CD上，BG=DH.求证：DF=BE

查看试题解析
16. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．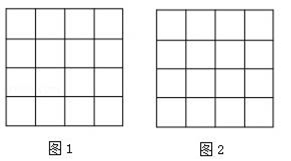

(1)、在图1中，画一个直角三角形，使它们的三边长都是无理数；

(2)、在图2中，画一个正方形，使它的面积是10．

查看试题解析
17. 如图，在ΔABC中，∠B=45°，∠C=60°，AC=8，求

(1)、边BC上的高；

(2)、ΔABC的面积．

查看试题解析
18. 如图，在平行四边形ABCD中，点E，F在对角线AC上，且AE=CF。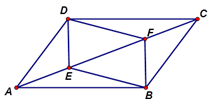

(1)、求证：四边形DEBF是平行四边形；

(2)、若DE=3，CD=4，∠EDC=90°，当四边形DEBF是菱形时，AE的长为多少？

查看试题解析
19. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一式子的平方，如 $4 + 2 \sqrt{3} = {(1 + \sqrt{3})}^{2}$ ，然后小明以进行了以下探索：
设 $a + b \sqrt{3} = {(m + n \sqrt{3})}^{2}$ （其中a，b，m，n均为整数），则有 $a + b \sqrt{3} = m^{2} + 3 n^{2} + 2 m n \sqrt{3}$ ，所以 $a = m^{2} + 3 n^{2}$ ， $b = 2 m n$ ，这样小明找到了一种类似 $a + b \sqrt{3}$ 的式子化为平方式的方法．

请仿照小明的方法探索解决下列问题：

(1)、当a，b，m，n均为整数时，若 $a + b \sqrt{5} = {(m + n \sqrt{5})}^{2}$ ，则a= ， b=；

(2)、请找一组正整数，填空：+ $\sqrt{5}$ =（+） $^{2}$ ；

(3)、若 $a + 4 \sqrt{5} = {(m + n \sqrt{5})}^{2}$ ，且a，m，n均为正整数，求a的值．

查看试题解析
20. 如图，在边长为1的正方形ABCD中，动点E，F分别在边AB，CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A，D重合），点C落在点N处，MN与CD交于点P，设BE=x．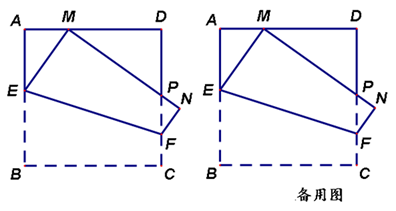

(1)、当AM= $\frac{1}{3}$ 时，求x的值；

(2)、随着点M在边AD上位置的变化，ΔPDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；

(3)、若AM=a，四边形BEFC的面积为S，求S与a之间的函数表达式．

查看试题解析

三、填空题

21. 如图，请你添加一个适当的条件，使平行四边形ABCD成为矩形。（答出一个即可）

查看试题解析
22. 如图，OA=OB，点C在数轴上表示的数为2，且有BC垂直于数轴，若BC=1，则数轴上点A表示的数是。

查看试题解析
23. 在ΔABC中，AB= $\sqrt{41}$ ，AC=5，若BC边上的高等于4，则BC的长为

查看试题解析