广西壮族自治区贵港市港南区2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-24 类型:期末考试
一、单选题
-
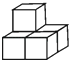
1. 2的倒数是( )。A、2 B、 C、 D、-22. 空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图是( )A、扇形图 B、条形图 C、折线图 D、直方图3. 下列运算中,正确的是( )A、 B、 C、 D、4. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 已知x:y:z=3:4:6,则 的值为( )A、 B、1 C、 D、6. 正比例函数y=2x和反比例函数 的一个交点为(1,2),则另一个交点为( )A、(﹣1,﹣2) B、(﹣2,﹣1) C、(1,2) D、(2,1)7. 在 中, , ,则 的值等于( )A、 B、 C、 D、 或8. 将抛物线y=(x-2)2+1向左平移2个单位,得到的新抛物线顶点坐标是( )A、 B、 C、 D、9. 如图, 中, ,若 , ,则 边的长是( )
5. 已知x:y:z=3:4:6,则 的值为( )A、 B、1 C、 D、6. 正比例函数y=2x和反比例函数 的一个交点为(1,2),则另一个交点为( )A、(﹣1,﹣2) B、(﹣2,﹣1) C、(1,2) D、(2,1)7. 在 中, , ,则 的值等于( )A、 B、 C、 D、 或8. 将抛物线y=(x-2)2+1向左平移2个单位,得到的新抛物线顶点坐标是( )A、 B、 C、 D、9. 如图, 中, ,若 , ,则 边的长是( )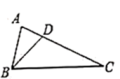 A、2 B、4 C、6 D、810. 如图,点A,B,C在圆O上,若∠BOC=72°,则∠BAC的度数是( ).
A、2 B、4 C、6 D、810. 如图,点A,B,C在圆O上,若∠BOC=72°,则∠BAC的度数是( ). A、72° B、54° C、36° D、18°11. 如图,在矩形 中, , , 是 边上一动点(不含端点 ),连接 , 是 边上一点,设 ,若存在唯一点 ,使 ,则 的值是( )
A、72° B、54° C、36° D、18°11. 如图,在矩形 中, , , 是 边上一动点(不含端点 ),连接 , 是 边上一点,设 ,若存在唯一点 ,使 ,则 的值是( )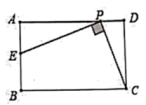 A、 B、 C、3 D、612. 如图,点 是正方形 的边 延长线一点,连接 交 于 ,作 , 交 的延长线于 ,连接 ,当 时,作 于 ,连接 ,则 的长为( )
A、 B、 C、3 D、612. 如图,点 是正方形 的边 延长线一点,连接 交 于 ,作 , 交 的延长线于 ,连接 ,当 时,作 于 ,连接 ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算: .14. 若tan(α–15°)= ,则锐角α的度数是 .15. 若a是方程 的解,计算: =.16. 如图,已知△ADE∽△ABC,且AD=3,DC=4,AE=2,则BE=.
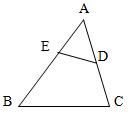 17. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .
17. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .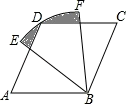 18. 如图,在 轴的正半轴上依次截取 ,过点 分别作 轴的垂线与反比例函数 的图象相交于点 ,得直角三角形 、 , , , ,并设其面积分别为 ,则 ( 的整数)
18. 如图,在 轴的正半轴上依次截取 ,过点 分别作 轴的垂线与反比例函数 的图象相交于点 ,得直角三角形 、 , , , ,并设其面积分别为 ,则 ( 的整数)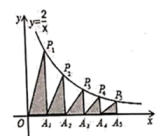
三、解答题
-
19.
(1)、计算:
(2)、先化简,再求值: ,其中 .20. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).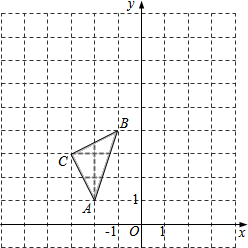 (1)、画出△ABC绕点B逆时针旋转90°得到的△A1BC1 .(2)、以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标 .21. 如图,一次函数 的图象与反比例函数 的图象交于点 , ,交y轴于点B,交x轴于点D.
(1)、画出△ABC绕点B逆时针旋转90°得到的△A1BC1 .(2)、以原点O为位似中心,位似比为2:1,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标 .21. 如图,一次函数 的图象与反比例函数 的图象交于点 , ,交y轴于点B,交x轴于点D.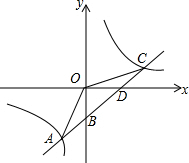 (1)、求一次函数 与反比例函数 的函数关系式;(2)、连结OA、OC,求 的面积;22. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
(1)、求一次函数 与反比例函数 的函数关系式;(2)、连结OA、OC,求 的面积;22. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.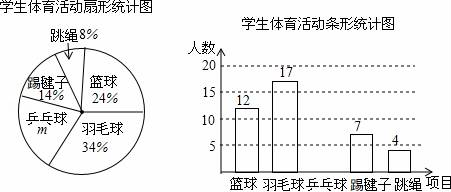 (1)、m=%,这次共抽取了名学生进行调查;并补全条形图;
(1)、m=%,这次共抽取了名学生进行调查;并补全条形图;
(2)、请你估计该校约有 名学生喜爱打篮球;
(3)、现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?23. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为 万元/辆,经销一段时间后发现:当该型号汽车售价定为 万元/辆时,平均每周售出 辆;售价每降低 万元,平均每周多售出 辆.(1)、当售价为 万元/辆时,平均每周的销售利润为万元;(2)、若该店计划平均每周的销售利润是 万元,为了尽快减少库存,求每辆汽车的售价.24. 在 中, , 平分 , 是边 上一点,以 为直径的 经过点 ,且交 于点 .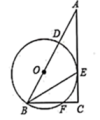 (1)、求证: 是 的切线;(2)、若 , 的半径为5,求 的长.25. 如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)、求证: 是 的切线;(2)、若 , 的半径为5,求 的长.25. 如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).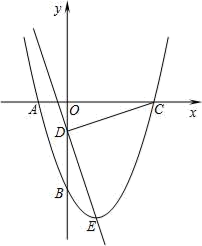 (1)、求抛物线的函数解析式;(2)、点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)、在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.26. 已知四边形 和四边形 都是正方形,且 .
(1)、求抛物线的函数解析式;(2)、点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)、在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.26. 已知四边形 和四边形 都是正方形,且 .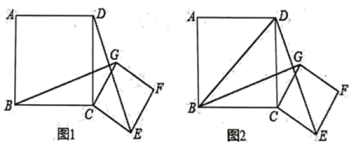 (1)、如图1,连接 .求证: ;(2)、如图2,将正方形 绕着点 旋转到某一位置时恰好使得 , .求 的度数;(3)、在(2)的条件下,当正方形 的边长为 时,请直接写出正方形 的边长.
(1)、如图1,连接 .求证: ;(2)、如图2,将正方形 绕着点 旋转到某一位置时恰好使得 , .求 的度数;(3)、在(2)的条件下,当正方形 的边长为 时,请直接写出正方形 的边长.