广西壮族自治区桂林市2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-02-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，能表示 $y$ 是 $x$ 的反比例函数的是（）

A、 $y = 2 x$ B、 $y = \frac{2}{x}$ C、 $y = x^{2}$ D、 $y = x - 1$

查看试题解析
2. 一元二次方程 $x^{2} = 9$ 的解是（）

A、 $x = 3$ B、 $x = - 3$ C、 $x_{1} = 3$ ， $x_{2} = - 3$ D、 $x_{1} = \sqrt{3}$ ， $x_{2} = - \sqrt{3}$

查看试题解析
3. 下列各组长度的线段（单位： $cm$ ）中，成比例线段的是（）

A、1，2，3，4 B、1，2，3，6 C、2，3，4，5 D、1，3，5，10

查看试题解析
4. 今年某市扶贫办对贫困户进行精准扶贫，效果显著.为了解他们后续的收入是否稳定，则工作人员需了解贫困户收入的（）

A、方差 B、众数 C、平均数 D、频数

查看试题解析
5. 若关于 $x$ 的一元二次方程 $x^{2} - 4 x + 2 m = 0$ 的常数项是4，则 $m$ 等于（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，△ABC，∠B=90°，AB=3，BC=4，则cosA等于（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
7. 已知点 $(- 2, y_{1})$ ， $(- 1, y_{2})$ ， $(1, y_{3})$ 都在反比例函数 $y = \frac{1}{x}$ 的图像上.下列结论中正确的是（）

A、 $y_{3} > y_{1} > y_{2}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{1} > y_{2} > y_{3}$ D、 $y_{2} > y_{3} > y_{1}$

查看试题解析
8. 下列命题中，是真命题的是（）

A、直角三角形都相似 B、等腰三角形都相似 C、矩形都相似 D、正方形都相似

查看试题解析
9. 如图，菱形 $A B C D$ 的边长为2， $∠ B = 45 °$ ， $A E ⊥ B C$ ，则这个菱形的面积是（）

A、4 B、8 C、 $2 \sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
10. 某单位要组织篮球邀请赛，每两队之间都要赛一场且只赛一场，计划安排15场比赛，设比赛组织者应邀请 $x$ 个队参赛，根据题意，可列方程（）

A、 $x (x + 1) = 15$ B、 $x (x - 1) = 15$ C、 $\frac{1}{2} x (x + 1) = 15$ D、 $\frac{1}{2} x (x - 1) = 15$

查看试题解析
11. 某数学活动小组在利用太阳光线测量某棵树 $A B$ 的高度时，发现树 $A B$ 的影子不全落在地面上，有一部分影子落在教学楼的墙壁上.经测量，落在墙壁上影高 $C D$ 为2米，落在地面上的影长 $B C$ 为5米，同一时间测得8米高的国旗杆影长是4米，则树高为（）

A、8米 B、10米 C、12米 D、14米

查看试题解析
12. 如图，在 $Δ A B C$ 中， $∠ A = 15 °$ ， $A B = 2$ ， $P$ 为 $A C$ 边上的一个动点（不与 $A$ 、 $C$ 重合），连接 $B P$ ，则 $\frac{\sqrt{2}}{2} A P + P B$ 的最小值是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{6}}{2}$ D、2

查看试题解析

二、填空题

13. 张强随机调查了他所在班级7名同学每天的睡眠时间（小时）为：7，7，8，8，8，9，9，则估计该班学生的平均睡眠时间约为小时.

查看试题解析
14. 已知 $Δ A B C ∽ Δ D E F$ ，且 $A B : D E = 1 : 2$ ，则 $Δ A B C$ 的周长与 $Δ D E F$ 的周长之比是.

查看试题解析
15. 如图，点 $B$ 是反比例函数 $y = \frac{k}{x}$ 在在第一象限内的图象上的点，若矩形 $O A B C$ 的面积为2，则 $k =$ .

查看试题解析
16. 若关于 $x$ 的一元二次方程 $a x^{2} + x - 2 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是.

查看试题解析
17. 如图，在 $Rt Δ A B C$ 中， $∠ C = 90 °$ ， $A C = B C$ ， $B C ∥ x$ 轴，点 $A$ 、 $B$ 都在反比例函数 $y = \frac{10}{x}$ 上，点 $C$ 在反比例函数 $y = \frac{4}{x}$ 上，则 $A B =$ .

查看试题解析
18. 如图， $A D$ 是 $Δ A B C$ 的中线， $E$ 是 $A D$ 上一点， $B E$ 的延长线交 $A C$ 于 $F$ ， $Δ A B E$ 的面积与 $Δ D B E$ 的面积之比是 $1： 3$ ，且 $A F = 2$ ，则 $F C =$ .

查看试题解析

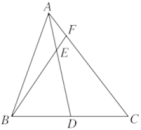
三、解答题

19. 计算： ${(\frac{1}{3})}^{- 1} - {(π - 3)}^{0} + 2 \sin 30 ° - | - 1 |$ .

查看试题解析
20. 解方程： $x^{2} - 2 x - 8 = 0$

查看试题解析
21. 如图，在边长为1个单位长度的小正方形网格中， $Δ A B C$ 的顶点均在格点上，在建立平面直角坐标系后，点 $A$ 的坐标为 $(1 ， 1)$ .

(1)、将 $Δ A B C$ 向左平移3个单位得到 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ；

(2)、在第三象限内，以 $O$ 为位似中心，将 $Δ A B C$ 放大到原大的2倍，画出放大后对应的 $Δ A_{2} B_{2} C_{2}$ ；

(3)、写出 $A_{2}$ 的坐标， $C_{2}$ 的坐标.

查看试题解析
22. 为了解学生对70周年国庆阅兵仪式直播的收看情况，某校对部分学生进行了一次调査，调査直播收看情况分三种：A．全程收看直播；B．观看了一部分直播；C．没有观看.学校学生会将调査数据进行了整理，并绘制了如下两幅不完整的统计图，请根据相关信息，解答下列问题：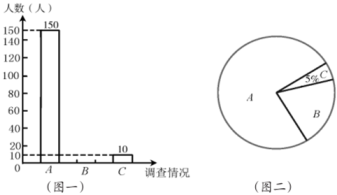

(1)、本次活动共调查了名学生；

(2)、图二中 $B$ 区域的圆心角的度数为；

(3)、补全图；

(4)、若该校学生共有3000名，请估计该校学生全程收看直播的人数是多少？

查看试题解析
23. 某服装店出售某品牌的棉衣，进价为100元/件，当售价为150元/件时，平均每天可卖30件；为了增加利润和减少库存，商店决定降价销售.经调査，每件每降价1元，则每天可多卖2件.

(1)、若每件降价20元，则平均每天可卖件.

(2)、现要想平均每天获利2000元，且让顾客得到实惠，求每件棉衣应降价多少元？

查看试题解析
24. 如图，正在海岛 $C$ 西南方向20海里作业的海监船 $A$ ，收到位于其正东方向渔船 $B$ 发出的遇险求救信号，已知渔船 $B$ 位于海岛 $C$ 的南偏东 $30 °$ 方向，海岛 $C$ 周围13海里内都有暗礁.（参考数据 $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ）

(1)、如果海监船 $A$ 沿正东方向前去救援是否有触礁的危险？

(2)、求海监船 $A$ 与渔船 $B$ 的距离.（结果精确到0.1海里）

查看试题解析
25. 如图，一次函数 $y_{1} = k x + b$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于第一象限 $C (1 ， 4)$ ， $D (4 ， a)$ 两点，与坐标轴交于 $A$ 、 $B$ 两点，连结 $O C$ ， $O D$ .

(1)、求 $y_{1}$ 与 $y_{2}$ 的函数解析式；

(2)、将直线 $A B$ 向上平移 $n$ 个单位到直线 $A^{'} B^{'}$ ，此时，直线 $A B$ 上恰有一点 $G$ 满足 $G C ∥ O D$ ， $G D ∥ O C$ ，求 $n$ 的值.

查看试题解析
26. 在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 8$ ， $F$ 是 $B C$ 边上的中点，动点 $E$ 在边 $A D$ 上，连接 $E F$ ，过点 $F$ 作 $F P ⊥ E F$ 分别交射线 $A D$ 、射线 $C D$ 于点 $P$ 、 $Q$ .

(1)、如图1，当点 $P$ 与点 $Q$ 重合时，求 $P F$ 的长；

(2)、如图2，当点 $Q$ 在线段 $C D$ 上（不与 $C$ ， $D$ 重合）且 $\tan P = \frac{1}{2}$ 时，求 $A E$ 的长；

(3)、线段 $P F$ 将矩形分成两个部分，设较小部分的面积为 $y$ ， $A E$ 长为 $x$ ，求 $y$ 与 $x$ 的函数关系式.

查看试题解析