广西壮族自治区来宾市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-24 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、-2019 D、20192. 把一副三角尺按如图所示拼在一起,则 等于( )
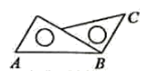 A、 B、 C、 D、3. 若 与 是同类项,则 , 的值分别是( )A、 , B、 , C、 , D、 ,4. 已知a=b,下列等式不一定成立的是( )A、a+c=b+c B、c﹣a=c﹣b C、ac=bc D、5. 数据1.38亿用科学记数法可表示为( )A、 B、 C、 D、6. 下列解方程变形正确的是( )A、由方程 ,得 B、由方程 ,得 C、由方程 ,得 D、由方程 ,得7. 多项式x2+3x﹣2中,下列说法错误的是( )A、这是一个二次三项式 B、二次项系数是1 C、一次项系数是3 D、常数项是28. 根据下图,下列说法中不正确的是( )
A、 B、 C、 D、3. 若 与 是同类项,则 , 的值分别是( )A、 , B、 , C、 , D、 ,4. 已知a=b,下列等式不一定成立的是( )A、a+c=b+c B、c﹣a=c﹣b C、ac=bc D、5. 数据1.38亿用科学记数法可表示为( )A、 B、 C、 D、6. 下列解方程变形正确的是( )A、由方程 ,得 B、由方程 ,得 C、由方程 ,得 D、由方程 ,得7. 多项式x2+3x﹣2中,下列说法错误的是( )A、这是一个二次三项式 B、二次项系数是1 C、一次项系数是3 D、常数项是28. 根据下图,下列说法中不正确的是( ) A、图①中直线 经过点 B、图②中直线 , 相交于点 C、图③中点 在线段 上 D、图④中射线 与线段 有公共点9. 下列调查工作需采用普查方式的是( )A、环保部门对长江某段水域的水污染情况的调查 B、电视台对正在播出的某电视节目收视率的调查 C、质检部门对各厂家生产的电池使用寿命的调查 D、企业在给职工做工作服前进行的尺寸大小的调查.10. 下列各组运算中,其计算结果最小的是( )A、 B、 C、 D、11. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件作服装仍可获利15元,则这种服装每件的成本是( )A、120元 B、125元 C、135元 D、140元12. 将一个边长为 的正方形纸片(图①)剪去两个小长方形,得到一个“
A、图①中直线 经过点 B、图②中直线 , 相交于点 C、图③中点 在线段 上 D、图④中射线 与线段 有公共点9. 下列调查工作需采用普查方式的是( )A、环保部门对长江某段水域的水污染情况的调查 B、电视台对正在播出的某电视节目收视率的调查 C、质检部门对各厂家生产的电池使用寿命的调查 D、企业在给职工做工作服前进行的尺寸大小的调查.10. 下列各组运算中,其计算结果最小的是( )A、 B、 C、 D、11. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件作服装仍可获利15元,则这种服装每件的成本是( )A、120元 B、125元 C、135元 D、140元12. 将一个边长为 的正方形纸片(图①)剪去两个小长方形,得到一个“ ”的图案(图②),再将剪下的两个小长方形拼成一个新的长方形(图③),新长方形的周长可表示为( )
”的图案(图②),再将剪下的两个小长方形拼成一个新的长方形(图③),新长方形的周长可表示为( ) 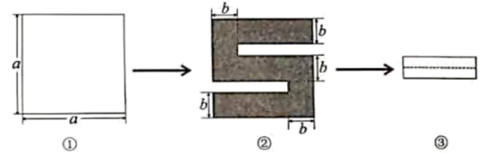 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 单项式7a3b2的次数是 .
14. 用式子表示“ 的3倍与 的 的和”,结果是.15. 比较大小: .(填“ ”、“ ”或“ ”)16. 有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人.设大和尚有 人,则可列一元一次方程为.17. 有理数 , 在数轴上的位置如图所示,则 .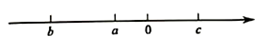 18. 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4…,当字母C第2n-1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).
18. 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4…,当字母C第2n-1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).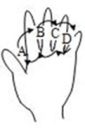
三、解答题
-
19.(1)、计算: ;(2)、解方程: .20. 已知一个角的余角比这个角的补角的 小 ,求这个角的余角和补角的度数.21. 先化简,再求值: ,其中 , .22. 为保护环境,节约资源,从今年6月1日起国家禁止超市、商场、药店为顾客提供免费塑料袋,为解决顾客购物包装问题,心连心超市提供了A自带购物袋;B租借购物篮;C购买环保袋;D徒手携带,四种方式供顾客选择.该超市把6月1日、2日两天的统计结果绘成如图的条形统计图和6月1日的扇形统计图,请你根据图形解答下列问题:
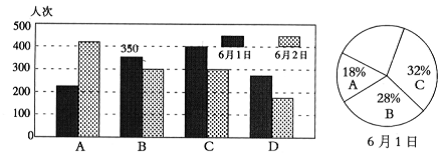 (1)、请将6月1日的扇形统计图补充完整.(2)、根据统计图求6月1日在该超市购物总人次和6月1日自带购物袋的人次.(3)、比较两日的条形图,你有什么发现?请用一句话表述你的发现.23. 一块三角尺的形状和尺寸如图所示,直角边的边长为 ,圆孔的半径为 .
(1)、请将6月1日的扇形统计图补充完整.(2)、根据统计图求6月1日在该超市购物总人次和6月1日自带购物袋的人次.(3)、比较两日的条形图,你有什么发现?请用一句话表述你的发现.23. 一块三角尺的形状和尺寸如图所示,直角边的边长为 ,圆孔的半径为 . (1)、求阴影部分的面积 ;(2)、当 , 时,求 的值( 取3.14).24. 如图,点 , , , , 在同一条直线上, , 为 的中点, .
(1)、求阴影部分的面积 ;(2)、当 , 时,求 的值( 取3.14).24. 如图,点 , , , , 在同一条直线上, , 为 的中点, .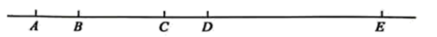 (1)、图中共有直线条,线段条,射线条;(2)、求线段 的长度.25. 某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元;经粗加工后销售,每吨利润4000元;经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨;但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜
(1)、图中共有直线条,线段条,射线条;(2)、求线段 的长度.25. 某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元;经粗加工后销售,每吨利润4000元;经精加工后销售,每吨利润7000元.当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果对蔬菜进行精加工,每天可加工6吨;但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,请说说理由.
26. 以直线 上点 为端点作射线 ,使 ,将直角 的直角顶点放在点 处.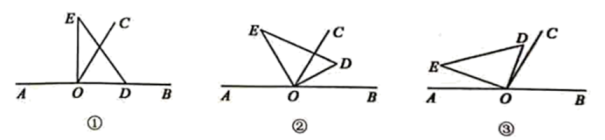 (1)、若直角 的边 在射线 上(图①),求 的度数;(2)、将直角 绕点 按逆时针方向转动,使得 所在射线平分 (图②),说明 所在射线是 的平分线;(3)、将直角 绕点 按逆时针方向转动到某个位置时,恰好使得 (图③),求 的度数.
(1)、若直角 的边 在射线 上(图①),求 的度数;(2)、将直角 绕点 按逆时针方向转动,使得 所在射线平分 (图②),说明 所在射线是 的平分线;(3)、将直角 绕点 按逆时针方向转动到某个位置时,恰好使得 (图③),求 的度数.