广西壮族自治区柳州市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-02-24 类型:期末考试
一、单选题
-
1. 下列汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中靶心 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是180°3. 下列方程属于一元二次方程的是( )A、3x-1=0 B、x3-4x=3 C、x2+2x-1=0 D、4. 抛物线 y=(x-1)2+2的顶点坐标是( )
2. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中靶心 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是180°3. 下列方程属于一元二次方程的是( )A、3x-1=0 B、x3-4x=3 C、x2+2x-1=0 D、4. 抛物线 y=(x-1)2+2的顶点坐标是( )
A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)5.如图,四边形ABCD是⊙O的内接四边形,∠B=70°,则∠D的度数是( )
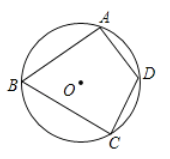 A、110° B、90° C、70° D、50°6. 点 (2,4) 在反比例函数 的图象上,下列各点也在此函数图象上的是( )
A、110° B、90° C、70° D、50°6. 点 (2,4) 在反比例函数 的图象上,下列各点也在此函数图象上的是( )
A、 B、
B、 C、
C、 D、
D、 7. 若关于 x 的一元二次方程 x2-x-m=0的一个根是 x=1 ,则 m 的值是( )
7. 若关于 x 的一元二次方程 x2-x-m=0的一个根是 x=1 ,则 m 的值是( )
A、 B、
B、 C、
C、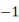 D、
D、 8. 修建一个面积为 100 平方米的矩形花园,它的长比宽多10米,设宽为 x米,可列方程为( )
8. 修建一个面积为 100 平方米的矩形花园,它的长比宽多10米,设宽为 x米,可列方程为( )
A、x(x-10)=100 B、2x+2(x-10)=100 C、2x+2(x+10)=100 D、x(x+10)=1009. 如图,从圆 O 外一点 引圆 P 的两条切线 PA , PB ,切点分别为 A , B .如果 ∠APB=60°, PA=8 ,那么圆 O 的半径是( ) A、4 B、 C、 D、10. 如图,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
A、4 B、 C、 D、10. 如图,点C在反比例函数y= (x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 点A(﹣2,3)关于原点对称的点的坐标是 .12. 一元二次方程x(x﹣3)=0的解是 .13. 在“山清水秀地干净”这句话中任选一个汉字,这个字是“清”的概率为.14. 已知圆锥的底面半径为 3cm ,母线长为 5cm ,则圆锥的侧面积是 cm2 (结果用含 π 的式子表示).
15. 已知二次函数 y=(x-h)2+3,当 x<2 时, y 随 x 的增大而减小,则 h 的取值范围是.
16. 如图,在菱形 ABCD 中, AB=2 , ∠C=120° ,点 P 是平面内一点,且 ∠APB=90° ,则 DP 的最小值为.
三、解答题
-
17. 解方程: x2-2x-3=0.
18. 如图,在平面直角坐标系中,已知 △ABC 的三个顶点的坐标分别为 A(-4,3) 、 B(-3,1) 、 C(1-,3) .
①将△ABC 先向右平移 4 个单位长度、再向上平移 2 个单位长度,得到 △A1B1C1 , 画出 △A1B1C1 .
② △A2B2C2与 △ABC 关于原点 O 成中心对称,画出 △A2B2C2 .
19. 为了传承优秀传统文化,我校开展“经典诵读”比赛互动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母 A,B,C依次表示这三个诵读材料),将 A,B,C这三个字母分别写在 3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.求:
(1)、小明诵读《论语》的概率.
(2)、小明和小亮诵读两个不同材料的概率.
20. 如图,直线y= x+2与双曲线y= 相交于点A(m,3),与x轴交于点C. (1)、求双曲线的解析式;(2)、点P在x轴上,如果△ACP的面积为3,求点P的坐标.21. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)、求双曲线的解析式;(2)、点P在x轴上,如果△ACP的面积为3,求点P的坐标.21. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: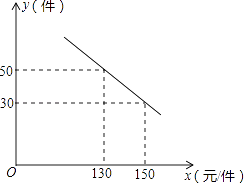 (1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?22. 如图,已知 AB 为⊙O的直径, F为 ⊙O 上一点, AC 平分 ∠BAF 且交 ⊙O 于点 C ,过点C 作 CD⊥AF 交AF 的延长线于点 D ,延长AB 、 DC 交于点 E ,连接 BC 、 CF .
(1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?22. 如图,已知 AB 为⊙O的直径, F为 ⊙O 上一点, AC 平分 ∠BAF 且交 ⊙O 于点 C ,过点C 作 CD⊥AF 交AF 的延长线于点 D ,延长AB 、 DC 交于点 E ,连接 BC 、 CF . (1)、求证: CD 是 ⊙O 的切线.
(1)、求证: CD 是 ⊙O 的切线.
(2)、求证: . 23. 如图,抛物线 y=-x2+4x交 x 轴于 O 、 B 两点, A 为抛物线上一点,且横纵坐标相等(原点除外), P 为抛物线上一动点,过 P 作 x 轴的垂线,垂足为D(a,0)(a>0) ,并与直线 OA 交于点 C .
. 23. 如图,抛物线 y=-x2+4x交 x 轴于 O 、 B 两点, A 为抛物线上一点,且横纵坐标相等(原点除外), P 为抛物线上一动点,过 P 作 x 轴的垂线,垂足为D(a,0)(a>0) ,并与直线 OA 交于点 C . (1)、求 A 、 B 两点的坐标.
(1)、求 A 、 B 两点的坐标.
(2)、当点 P 在线段 OA 上方时,过 P 作 x 轴的平行线与直线 OA 相交于点 E ,求 △PCE 周长的最大值及此时 P 点的坐标.