人教A版(2019)数学必修第一册5.3 诱导公式
试卷更新日期:2020-02-23 类型:同步测试
一、单选题
-
1. 等于( )A、1 B、﹣1 C、 D、2. ( )A、 B、 C、 D、3. 已知 ,则 ( )A、 B、 C、 D、04. 已知 ,则 的值等于( )
A、 B、- C、 D、±5. 已知 ,则 ( )A、 B、 C、 D、6. 已知sin(π+θ)=﹣ cos(2π﹣θ),|θ|< ,则θ等于( )A、﹣ B、﹣ C、 D、7. 若sin(π﹣α)=﹣ ,且α∈(π, ),则sin( +α)=( )A、﹣ B、﹣ C、 D、8. 已知 ,则 ( )
A、 B、 C、 D、9. 已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x﹣y=0上,则 等于( )A、﹣ B、 C、0 D、10. 化简 的结果是( )A、1 B、sinα C、﹣tanα D、tanα11. 已知tan100°=K,则cos10°=( )A、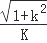 B、
B、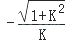 C、
C、 D、
D、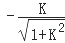 12. 已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2002)=3,则f(2003)的值是( )A、﹣1 B、﹣2 C、﹣3 D、113. 已知f(α)= ,则f(﹣ )的值为( )A、 B、﹣ C、 D、﹣14. 设角 的值等于( )A、 B、﹣ C、 D、﹣
12. 已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2002)=3,则f(2003)的值是( )A、﹣1 B、﹣2 C、﹣3 D、113. 已知f(α)= ,则f(﹣ )的值为( )A、 B、﹣ C、 D、﹣14. 设角 的值等于( )A、 B、﹣ C、 D、﹣二、填空题
-
15. 计算: .16. 已知 为锐角,且 ,则 .17. 化简 的结果为 .18. sin(﹣ )+cos(﹣ )+tan(﹣ )= .19. 已知角 的顶点在坐标原点,始边与 轴正半轴重合,终边在直线 ,则 .
三、解答题