初中数学浙教版八年级下册第三章 数据分析初步 章末检测
试卷更新日期：2020-02-20 类型：单元试卷
一、单选题
-
1. 某公司欲招聘一名工作人员，对甲应聘者进行面试和笔试，面试成绩为85分，笔试成绩为90分
若公司分别赋予面试成绩和笔试成绩7和3的权，则下列算式表示甲的平均成绩的是（ ） A、
B、 
C、 
D、
2. 某班学生军训射击，有m人各打中a环，n人各打中b环，那么该班打中a环和b环学生的平均环数是（ ）A、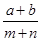
B、
C、
D、
3. 为了解某班学生每天的睡眠情况，随机选择该班5名学生进行调查．在一段时间里，平均每人每天的睡眠时间统计如下(单位：小时)：6，8，8，7，9．由此估计该班学生平均每人每天的睡眠时间为（ ）A、7小时 B、7.5小时 C、7.6小时 D、8小时4. 若一组数据2，3，x，5，7的众数为7，则这组数据的中位数为（ ）A、2 B、3 C、5 D、75. 2018年某中学举行的春季田径径运动会上，参加男子跳高的15名运动员的成绩如表所示：这些运动员跳高成绩的中位数和众数分别是（ ）
A、1.70 ，1.65 B、1.70 ，1.70 C、1.65 ，1.60 D、3 ，46. 一组数据1，2，3，4，4，10．去掉10，剩下的数据原数据相比，不变的是（ ）A、平均数 B、中位数 C、众数 D、平均数和众数7. 图1，图2分别是某厂六台机床十月份第一天和第二天生产零件数的统计图，与第一天相比，第二天六台机床生产零件数的平均数与方差的变化情况是（ ）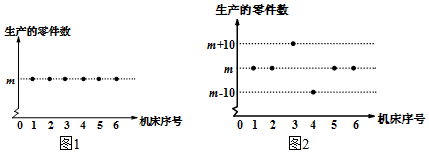
A、平均数变大，方差不变 B、平均数变小，方差不变 C、平均数不变，方差变小 D、平均数不变，方差变大8. 甲、乙两名运动员进行射击练习，每人射击5次，成绩（单位：环）如下表所示：下列说法错误的是（ ）第1次
第2次
第3次
第4次
第5次
平均成绩
甲
7
▲
8
10
8
8
乙
7
8
8
9
8
▲
A、甲运动员的第2次射击成绩为7环 B、乙运动员的平均射击成绩为8环 C、甲运动员这5次射击成绩的方差为6 D、乙运动员的成绩更稳定9. 若一组数据x1＋1，x2＋1，…，xn＋1的平均数为17，方差为2，则另一组数据x1＋2，x2＋2，…，xn＋2的平均数和方差分别为（ ）A、17，2 B、18，2 C、17，3 D、18，310. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：尺码
39
40
41
42
43
平均每天销售数量/件
6
15
21
12
9
该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（ ）
A、平均数 B、中位数 C、方差 D、众数二、填空题
-
11. 8个数的平均数12，4个数的平均为18，则这12个数的平均数为.12. 一组数据a，b，c，d，e的平均数是7，则另一组数据a+2，b+2，c+2，d+2，e+2的平均数为.13. 一组数据1、3、4、5、x、9的众数和中位数相同，那么x的值是14. “植树节”时，九(1)班6个小组的植树棵数分别是：5，7，3，x，6，4.已知这组数据的众数是5，则该组数据的平均数是15. 已知一组数据0，1，2，2，x，3的平均数是2，则这组数据的方差是 ．16. 已知一组数据a、b、c、d. e方差为3，则另一组数据a+3，b+3，c+3，d+3，e+3的方差为 ，
三、综合题
-
17. 七（1）班共45名学生，在一次数学测试中以90分为标准，超过的记为正，不足的记为负，成绩如下：
人数
5
10
8
12
4
5
1
成绩
-1
+3
-2
+1
+10
0
-4
请你算出这次考试的平均成绩（精确到0.1分）
18. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的，如果期末评价成绩80分以上（含80分），则评为“优秀”．下面表中是小张和小王两位同学的成绩记录：完成作业
单元测试
期末考试
小张
70
90
80
小王
60
75
(1)、若按三项成绩的平均分记为期末评价成绩，请计算小张的期末评价成绩；(2)、若按完成作业、单元检测、期末考试三项成绩按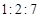
的权重来确定期末评价成绩． ①请计算小张的期末评价成绩为多少分？
②小王在期末（期末成绩为整数）应该最少考多少分才能达到优秀？
19. 某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图：
(1)、根据上图求出下表所缺数据；平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8
10
1.6
(2)、根据上表中的平均数、中位数和方差你认为哪班的成绩较好？并说明你的理由.20. 王老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的八年（1）班和八年（2）班进行了检测．如图所示表示从两班随机抽取的10名学生的得分情况：
(1)、利用图中提供的信息，补全如表：班级
平均分（分）
中位数（分）
众数（分）
八年（1）班
24
24
八年（2）班
24
(2)、你认为那个班的学生纠错的得分情况比较整齐一些，通过计算说明理由．21. 如图，甲、乙两人在一次射击比赛中击中靶的情况（击中靶中心“×”所在的圆面为10环，靶中各数字表示该数所在圆环被击中所得的环数），每人射击了6次．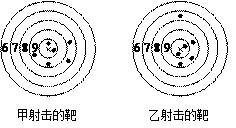
(1)、请用列表法将他俩的射击成绩统计出来；
(2)、请你运用所学的统计知识做出分析，从两个不同角度评价甲、乙两人的打靶成绩．
22. 某公司招聘职员两名，对甲、乙、丙、丁四名候选人进行了笔试和面试，各项成绩满分均为100分，然后再按笔试占60%，面试占40%计算候选人的综合成绩(满分为100分)他们的各项成绩如下表所示：
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)、这四名候选人面试成绩的中位数是。(2)、现得知候选人丙的综合成绩为87.6分，则表中x的值等于。(3)、求其余三名候选人的综合成绩，并以综合成绩排序确定所要招聘的前两名的人选。23. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；(2)、分别计算甲、乙六次测试成绩的方差；(3)、根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．24. 高尔基说：“书，是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况，某校随机抽查了部分学生阅读课外书册数的情况，并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.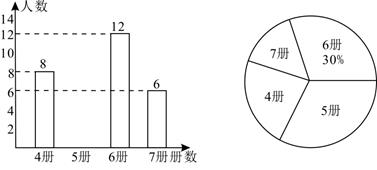
(1)、求条形图中丢失的数据，并写出阅读书册数的众数和中位数；(2)、根据随机抽查的这个结果，请估计该校1200名学生中课外阅读5册书的学生人数；(3)、若学校又补查了部分同学的课外阅读情况，得知这部分同学中课外阅读最少的是6册，将补查的情况与之前的数据合并后发现中位数并没有改变，试求最多补查了多少人？