初中数学浙教版八年级下册3.3 方差和标准差 基础巩固训练

试卷更新日期：2020-02-20 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

    甲

    乙

    丙

    丁

    平均数 x¯ （厘米）

    375

    350

    375

    350

    方差 s2

    12.5

    13.5

    2.4

    5.4

    要从中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 2. 甲、乙、丙、丁四人进行射击测试，经过测试，平均成绩均为 9.2 环，方差如下表所示：

    选手

    甲

    乙

    丙

    丁

    方差

    1.75

    2.93

    0.50

    0.40

    则在这四个选手中，成绩最稳定的是（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 3. 为了考察甲、乙两块地小麦的长势，分别从中抽取10株苗，测得苗高如下（单位：cm）：

    甲：12,13,14,15,10,16,13,11,15,11；乙：11,16,17,14,13,19,6,8,10,16.

    要比较哪块地小麦长得比较整齐，我们应选择的统计量是（  ）

    A、中位数 B、平均数 C、众数 D、方差

    查看试题解析

  • 4. 甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是1.28m，方差分别是s甲2＝0.60，s乙2＝0.62，s丙2＝0.58，s丁2＝0.45，则这四名同学跳高成绩最稳定的是（   ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 5. 一组数据：3、4、4、5，若添加一个数4，则发生变化的统计量是（ ）
    A、平均数 B、众数 C、中位数 D、标准差

    查看试题解析

  • 6. 甲，乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛，他们成绩的平均数、中位数、方差如下表所示，规定成绩大于等于95分为优异，则下列说法正确的是（   ）

    参加人数

    平均数

    中位数

    方差

    甲

    45

    94

    93

    5.3

    乙

    45

    94

    95

    4.8
    A、甲、乙两班的平均水平相同 B、甲、乙两班竞赛成绩的众数相同 C、甲班的成绩比乙班的成绩稳定 D、甲班成绩优异的人数比乙班多

    查看试题解析

  • 7. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数x（单位：千克）及方差S2（单位：千克2）如下表所示：

    甲

    乙

    丙

    丁

    x

    24

    24

    23

    20

    S2

    2.1

    1.9

    2

    1.9

    今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 8. 方差是刻画数据波动程度的量，对于一组数据x·x1·…xn ， 可用如下算式计算方差s2= 1n [（x1-5）2+（x2-5）2+.…+（xn-5）2]，其中“5”是这组数据的（   ）
    A、最小值 B、平均数 C、中位数 D、众数

    查看试题解析

  • 9. 已知一组数据的方差是3，则这组数据的标准差是（   ）
    A、3 B、3 C、32 D、9

    查看试题解析

  • 10. 如表记录了两位射击运动员的八次训练成绩：

    次数环数

    运动员

    第1次

    第2次

    第3次

    第4次

    第5次

    第6次

    第7次

    第8次

    甲

    10

    7

    7

    8

    8

    8

    9

    7

    乙

    10

    5

    5

    8

    9

    9

    8

    10

    根据以上数据，设甲、乙的平均数分别为 x甲¯ 、 x乙¯ ，甲、乙的方差分别为 s甲2 ， s乙2 ，则下列结论正确的是（    ）

    A、x甲¯=x乙¯ ， s甲2<s乙2 B、x甲¯=x乙¯ ， s甲2>s乙2 C、x甲¯>x乙¯ ， s甲2<s乙2 D、x甲¯<x乙¯ ， s甲2<s乙2

    查看试题解析

二、填空题

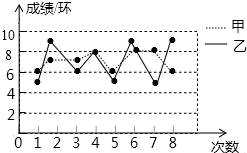
  • 11. 甲、乙两个篮球队队员身高的平均数都为2.07米，方差分别是S甲2、S乙2 ， 且S甲2＞S乙2 ， 则队员身高比较整齐的球队是.

    查看试题解析

  • 12. 已知一组数据5，8，10，x，9的众数是8，那么这组数据的方差是 。

    查看试题解析

  • 13. 设甲组数：1，1，2，5的方差为S甲2 ， 乙组数是：6，6，6，6的方差为S乙2 ， 则S甲2与S乙2的大小关系是S甲2S乙2（选择“＞”、“＜”或“=”填空）．

    查看试题解析

  • 14. 甲乙两人8次射击的成绩如图所示(单位：环)根据图中的信息判断，这8次射击中成绩比较稳定的是(填“甲”或“乙”)

    查看试题解析

三、解答题

  • 15. 给定一组数据：8，24，14，24，24，14．
    (1)、求出这组数据的平均数是、中位数是、众数是；
    (2)、计算这组数据的方差．

    查看试题解析

  • 16. 射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

    (1)、完成表中填空①；②；
    (2)、请计算甲六次测试成绩的方差；
    (3)、若乙六次测试成绩方差为 43 ，你认为推荐谁参加比赛更合适，请说明理由．

    查看试题解析

  • 17. 甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）： 

    甲：98，100，100，90，96，91，89，99，100，100，93

    乙：98，99，96，94，95，92，92，98，96，99，97

    (1)、他们的平均成绩分别是多少？
    (2)、甲、乙的11次单元测验成绩的标准差分别是多少？
    (3)、这两位同学的成绩各有什么特点？
    (4)、现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？

    查看试题解析