初中数学浙教版八年级下册3.1 平均数强化提升训练

试卷更新日期：2020-02-20 类型：同步测试

进入出卷网下载

一、中考演练

1. 某商场为了解产品A的销售情况，在上个月的销售记录中，随机抽取了5天A产品的销售记录，其售价x（元/件）与对应销量y（件）的全部数据如下表：
售价x（元/件）
90
95
100
105
110
销量y（件）
110
100
80
60
50
则这5天中，A产品平均每件的售价为（）

A、100元 B、95元 C、98元 D、97.5元

查看试题解析
2. 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核（考核的满分均为100分），三个方面的重要性之比依次为3：5：2．小王经过考核后所得的分数依次为90、88、83分，那么小王的最后得分是（）

A、87 B、87.5 C、87.6 D、88

查看试题解析
3. 某球员参加一场篮球比赛，比赛分4节进行，该球员每节得分如折线统计图所示，则该球员平均每节得分为（）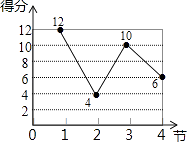

A、7分 B、8分 C、9分 D、10分

查看试题解析
4. 某中学规定学生的学期体育成绩满分为100分，其中早锻炼及体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%.小桐的三项成绩（百分制）依次为95，90，85.则小桐这学期的体育成绩是（）

A、88.5 B、86.5 C、90 D、90.5

查看试题解析
5. 某计算机程序第一次算得m个数据的平均数为x，第二次算得另外n个数据的平均数为y，则这m+n个数据的平均数等于。

查看试题解析
6. 为了解某班学生体育锻炼的用时情况，收集了该班学生一天用于体育锻炼的时间（单位：小时），整理成如图的统计图.则该班学生这天用于体育锻炼的平均时间为小时.

查看试题解析
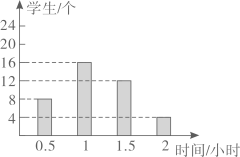7. 某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分，综合成绩笔试占40%，试讲占40%，面试占20%，则该名教师的综合成绩为分．

查看试题解析

二、提高训练

8. 如果两组数据x₁ ， x₂、……x_n；y₁ ， y₂……y_n的平均数分别为 $\bar{x}$ 和 $\bar{y}$ ，那么新的一组数据2x₁+y₁ ， 2x₂+y₂……2x_n+y_n的平均数是（）

A、2 $\bar{x}$ B、2 $\bar{y}$ C、2 $\bar{x}$ + $\bar{y}$ D、 $\frac{4 \bar{x} + \bar{y}}{2}$

查看试题解析
9. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
10. 小亮调查本班同学的身高后，将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值，但不包含最大值，比如第二小组的x满足145≤x＜150，其他小组的数据类似)．设班上学生身高的平均数为 $\bar{x}$ (单位：cm)，则 $\bar{x}$ 的取值范围是.

查看试题解析
11. 甲、乙、丙三人分别投资50万元、30万元、20万元成立一个股份公司，一年后亏损了12万，甲提出每人承担4万元的损失，你认为这个提议（填“合理”或“不合理”）.

查看试题解析
12. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析
13. 统计学规定：某次测量得到n个结果x₁ ， x₂ ， …，x_n.当函数y=(x-x₁)²+(x-x₂)²+…+(x-x_n)²取最小值时，对应x的值称为这次测量的“最佳近似值”.若某次测量得到5个结果分别为9.8，10.1，10.5，10.3，9.8，则这次测量的“最佳近似值”为.

查看试题解析
14. 市三个郊县的人数及人均耕地面积如下表：
这个市郊县的人均耕地面积是多少?(精确到0.01公顷)
小明求得这个市郊县的人均耕地面积为 $\bar{x} = \frac{0.15 + 0.21 + 0.18}{3}$ ，你认为小明的做法对吗？

查看试题解析

15.

(1)、在某次考试中，现有甲、乙、丙3名同学，共四科测试实际成绩如下表：(单位：分)

	语文	数学	英语	科学
甲	95	95	80	150
乙	105	90	90	139
丙	100	100	85	139

若欲从中表扬2人，请你从平均数的角度分析哪两人将被表扬?

(2)、为了体现学科差异，参与测试的语文、数学、英语科学实际成绩须以2：3：2：3的比例计入折合平均数．请你从折合平均数的角度分析哪两人将被表扬?

查看试题解析

16. 某公司欲招聘一名部门经理，对甲、乙、丙三名候选人进行了三项素质测试．各项测试成绩如表格所示：

测试项目	测试成绩
测试项目	甲	乙	丙
专业知识	74	87	90
语言能力	58	74	70
综合素质	87	43	50

(1)、如果根据三次测试的平均成绩确定人选，那么谁将被录用？

(2)、根据实际需要，公司将专业知识、语言能力和综合素质三项测试得分按4：3：1的比例确定每个人的测试总成绩，此时谁将被录用？

(3)、请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩，使得乙被录用，若重新设计的比例为x：y：1，且x+y+1＝10，则x＝， y＝．（写出x与y的一组整数值即可）．

查看试题解析

售价x（元/件）	90	95	100	105	110
销量y（件）	110	100	80	60	50

初中数学浙教版八年级下册3.1 平均数 强化提升训练

一、中考演练

二、提高训练

初中数学浙教版八年级下册3.1 平均数强化提升训练