初中数学浙教版九年级下册第二章 直线与圆的位置关系 章末检测
试卷更新日期：2020-02-20 类型：单元试卷
一、单选题
-
1. 已知⊙O的直径为4，圆心O到直线l的距离是4，则⊙O与直线l的关系是（ ）A、相交 B、相切 C、相离 D、相交或相切2. 平面内，⊙O的半径为1，点P到O的距离为2，过点P可作⊙O的切线条数为（ ）A、0条 B、1条 C、2条 D、无数条3. 如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2=8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现（ ）
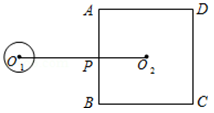A、3次 B、5次 C、6次 D、7次4. 已知∠BAC=45°，一动点O在射线AB上运动（点O与点A不重合），设OA=x，如果半径为1的⊙O与射线AC有公共点，那么x的取值范围是（ ）A、0<x≤1 B、1≤x< C、0<x≤ D、x>5. 如图，PA、PB为圆O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交圆O于点D，下列结论不一定成立的是（ ）
A、PA＝PB B、∠BPD＝∠APD C、AB⊥PD D、AB平分PD6. 如图，⊙O与正方形ABCD是两边AB，AD相切，DE与⊙O相切于点E，若正方形ABCD的边长为5，DE＝3，则tan∠ODE为（ ）
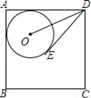A、 B、 C、 D、7. 已知直角三角形的两条直角边分别为12cm和16cm，则这个直角三角形内切圆的半径是（ ）A、2cm B、3cm C、4cm D、5cm8. 如图，一块直角三角板和一张光盘竖放在桌面上，其中A是光盘与桌面的切点，∠BAC＝60°，光盘的直径是80cm，则斜边AB被光盘截得的线段AD长为（ ）
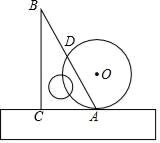A、20 cm B、40 cm C、80cm D、80 cm9. 如图，在▱ABCD中， ， ， 分别切边AB，AD于点E，F，且圆心O恰好落在DE上 现将 沿AB方向滚动到与边BC相切 点O在 的内部 ，则圆心O移动的路径长为
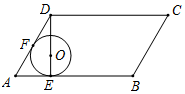A、4 B、6 C、
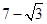D、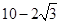
10. 一个直角三角形的斜边长为8，内切圆半径为1，则这个三角形的周长等于（ ）A、21 B、20 C、19 D、18二、填空题
-
11. 如图，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B，若∠ABP＝35°，则∠P＝.
12. 如图所示， 内切△ABC ，切点分别为 ， ， ， 切 于 点，交 ， 于点 ， ，若△ABC 的周长为12，BC=2，则△ADE 的周长是 ．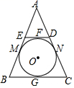
13. 如图，两个同心圆，大圆半径为5cm，小圆的半径为3cm，若大圆的弦AB与小圆相交，则弦AB的取值范围是 ．
14. 如图，已知⊙O是△ABC的内切圆，切点为D、E、F ， 如果AE=2，CD=1，BF=3，则内切圆的半径r= ．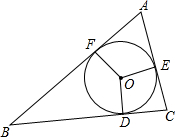
15. 如图，在 中， ， ， ， 是 的内切圆，点 是斜边 的中点，则 ．
16. 已知一块直角三角形钢板的两条直角边分别为30cm、40cm，能从这块钢板上截得的最大圆的半径为 ．
三、解答题
-
17. AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC．
①求证：DC为⊙O切线；
②若AD•OC＝8，求⊙O半径r．
18. 如图，已知在△ABC中．
(1)、请用圆规和直尺作出△ABC的内切圆⊙P；（保留作图痕迹，不写作法）(2)、若⊙P与AB、BC、AC 分别相切于点D、E、F，且AD＝1，△ABC的周长为12，求BC的长．19. 如图，过点P作PA，PB，分别与以OA为半径的半圆切于A，B，延长AO交切线PB于点C，交半圆与于点D.
(1)、若PC=5，AC=4，求BC的长；(2)、设DC：AD=1：2，求 的值.20. 如图，已知AB为⊙O的直径，BD为⊙O的切线，过点B的弦BC⊥OD交⊙O于点C，垂足为M.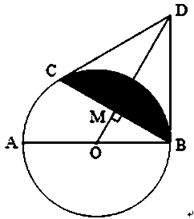
(1)、求证：CD是⊙O的切线；(2)、当BC=BD，且BD=6cm时，求图中阴影部分的面积（结果不取近似值）21. 如图，AB是半圆O的直径，过点O作弦AD的垂线交半圆O于点E，交AC于点C，使∠BED=∠C．
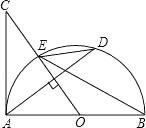(1)、判断直线AC与圆O的位置关系，并证明你的结论；(2)、若AC=8， ，求AD的长．22. 已知：如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以AE为直径的⊙O与BC边相切于点D，连结AD．
(1)、求证：AD是∠BAC的平分线；(2)、若AC= 3，BC=4，求⊙O的半径.23. 我们引入如下概念，定义；到三角形的两条边的距离相等的点，叫做此三角形的准内心，举例：如图1，PE⊥BC，若PE＝PD则P为△ABC的准内心
(1)、填空；根据准内心的概念，图1中的点P在∠BAC的上．(2)、应用；如图2，△ABC中，AC＝BC＝13，AB＝10，准内心P在AB上，求P到AC边的距离PD的长．(3)、探究；已知△ABC为直角三角形，AC＝BC＝6，∠C＝90°，准内心P在△ABC的边上，试探究PC的长．24. 阅读以下材料，并按要求完成相应地任务：莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家，在数学上经常见到以他的名字命名的重要常数，公式和定理，下面是欧拉发现的一个定理：在△ABC中，R和r分别为外接圆和内切圆的半径，O和I分别为其外心和内心，则 .
如图1，⊙O和⊙I分别是△ABC的外接圆和内切圆，⊙I与AB相切分于点F，设⊙O的半径为R，⊙I的半径为r，外心O（三角形三边垂直平分线的交点）与内心I（三角形三条角平分线的交点）之间的距离OI＝d，则有d2＝R2﹣2Rr．
下面是该定理的证明过程（部分）：
延长AI交⊙O于点D，过点I作⊙O的直径MN，连接DM，AN.
∵∠D=∠N，∠DMI=∠NAI(同弧所对的圆周角相等)，
∴△MDI∽△ANI，
∴ ，
∴ ①，
如图2，在图1(隐去MD，AN)的基础上作⊙O的直径DE，连接BE，BD，BI，IF，
∵DE是⊙O的直径，∴∠DBE=90°，
∵⊙I与AB相切于点F，∴∠AFI=90°，
∴∠DBE=∠IFA，
∵∠BAD=∠E(同弧所对圆周角相等)，
∴△AIF∽△EDB，
∴ ，∴ ②，
任务：
(1)、观察发现： ， (用含R，d的代数式表示)；(2)、请判断BD和ID的数量关系，并说明理由；(3)、请观察式子①和式子②，并利用任务(1)，(2)的结论，按照上面的证明思路，完成该定理证明的剩余部分；(4)、应用：若△ABC的外接圆的半径为5cm，内切圆的半径为2cm，则△ABC的外心与内心之间的距离为cm.