初中数学浙教版九年级下册2.3 三角形的内切圆 强化提升训练
试卷更新日期:2020-02-20 类型:同步测试
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC的内切圆,点D是斜边AB的中点,则cos∠ODA= ( )
 A、 B、 C、 D、2. 如图,点O是△ABC的内心,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+ ∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF= mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切.其中符合题意结论的个数是( )
A、 B、 C、 D、2. 如图,点O是△ABC的内心,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+ ∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF= mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切.其中符合题意结论的个数是( )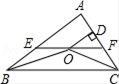 A、1个 B、2个 C、3个 D、4个3. 如图, 的顶点O是边长为2的等边 的重心, 的两边与 的边交于E , F , ,则 与 的边所围成阴影部分的面积是( )
A、1个 B、2个 C、3个 D、4个3. 如图, 的顶点O是边长为2的等边 的重心, 的两边与 的边交于E , F , ,则 与 的边所围成阴影部分的面积是( )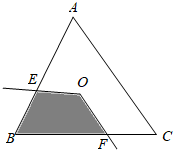 A、 B、 C、 D、4. 如图,有一三角形ABC的顶点B,C皆在直线L上,且其内心为I.今固定C点,将此三角形依顺时针方向旋转,使得新三角形A'B'C的顶点A′落在L上,且其内心为I′.若∠A<∠B<∠C,则下列叙述何者正确?( )
A、 B、 C、 D、4. 如图,有一三角形ABC的顶点B,C皆在直线L上,且其内心为I.今固定C点,将此三角形依顺时针方向旋转,使得新三角形A'B'C的顶点A′落在L上,且其内心为I′.若∠A<∠B<∠C,则下列叙述何者正确?( ) A、IC和 平行, 和L平行 B、IC和 平行, 和L不平行 C、IC和 不平行, 和L平行 D、IC和 不平行, 和L不平行5. 如图,AB是⊙O的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,∠ACB的角平分线交⊙O于点D , ∠BAC的平分线交CD于点E . 当点C从点M运动到点N时,则C、E两点的运动路径长的比是( )
A、IC和 平行, 和L平行 B、IC和 平行, 和L不平行 C、IC和 不平行, 和L平行 D、IC和 不平行, 和L不平行5. 如图,AB是⊙O的直径,M、N是弧AB(异于A、B)上两点,C是弧MN上一动点,∠ACB的角平分线交⊙O于点D , ∠BAC的平分线交CD于点E . 当点C从点M运动到点N时,则C、E两点的运动路径长的比是( ) A、 B、 C、 D、6. 如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )
A、 B、 C、 D、6. 如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )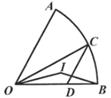 A、180°- β B、180°-β C、90°+ β D、90°+β7. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )
A、180°- β B、180°-β C、90°+ β D、90°+β7. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )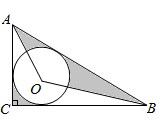
A、 B、 C、12 D、148. 已知在△ABC中,∠BAC=90°,M是边BC的中点,BC的延长线上的点N满足AM⊥AN.△ABC的内切圆与边AB,AC的切点分别为E,F,延长EF分别与AN,BC的延长线交于P、Q,则 =( )A、1 B、0.5 C、2 D、1.5二、填空题
-
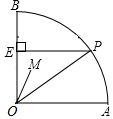
9. 如图,在圆心角为90°的扇形 中, , 为 上任意一点,过点 作 于点 ,设 为 的内心,当点 从点 运动到点 时,则内心 所经过的路径长为 .
 10. 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD= ,那么△ABC的内切圆半径为
10. 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD= ,那么△ABC的内切圆半径为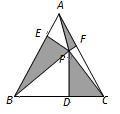 11. 如图,在 中,
11. 如图,在 中,⑴作AB和BC的垂直平分线交于点O;
⑵以点O为圆心,OA长为半径作圆;
⑶⊙O分别与AB和BC的垂直平分线交于点M,N;
⑷连接AM,AN,CM,其中AN与CM交于点P.
根据以上作图过程及所作图形,下列四个结论中,
① ; ② ;
③点O是 的外心 ; ④点P是 的内心.
所有正确结论的序号是.
 12. 如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为.
12. 如图,AB为弓形AB的弦,AB=2 ,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为.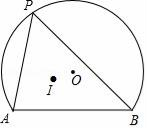
三、综合题
-
13. 如图,点 是 的内心, 的延长线和 的外接圆圆 相交于点 ,过 作直线 .
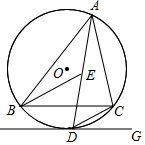 (1)、求证: 是圆 的切线;(2)、若 , ,求优弧 的长.14. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2).
(1)、求证: 是圆 的切线;(2)、若 , ,求优弧 的长.14. 如图,在△ABC中,∠ACB=90°,∠ABC=45°,BC=12cm,半圆O的直径DE=12cm.点E与点C重合,半圆O以2cm/s的速度从左向右移动,在运动过程中,点D、E始终在BC所在的直线上.设运动时间为x(s),半圆O与△ABC的重叠部分的面积为S(cm2).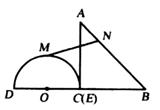 (1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?15. 如图
(1)、当x=0时,设点M是半圆O上一点,点N是线段AB上一点,则MN的最大值为 :MN的最小值为.(2)、在平移过程中,当点O与BC的中点重合时,求半圆O与△ABC重叠部分的面积S;(3)、当x为何值时,半圆O与△ABC的边所在的直线相切?15. 如图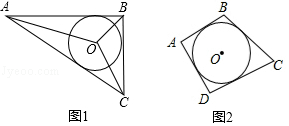 (1)、如图1,在面积为6的△ABC中,BC=3,AB=4,AC=5,求△ABC内切圆O的半径r的值.(2)、如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a、BC=b、CD=c、AD=d,求四边形的内切圆半径r的值.(3)、若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、……、an , 合理猜想其求内切圆半径r的公式(不需说明理由)16. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①
(1)、如图1,在面积为6的△ABC中,BC=3,AB=4,AC=5,求△ABC内切圆O的半径r的值.(2)、如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a、BC=b、CD=c、AD=d,求四边形的内切圆半径r的值.(3)、若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、……、an , 合理猜想其求内切圆半径r的公式(不需说明理由)16. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
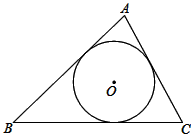 (1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .