上海市黄浦区2017-2018学年八年级下学期数学期中考试试卷

试卷更新日期：2020-02-19 类型：期中考试

进入出卷网下载

一、单选题

1. 一次函数y=kx+b的图象如图所示，当y＞3时，x的取值范围是（）

A、 $x < 0$ B、 $x > 0$ C、 $x < 2$ D、 $x > 2$ ．

查看试题解析
2. 下列关于 $x$ 的方程中，有实数根的是（）

A、x²+2x+3=0 B、 $x^{3} + 2 = 0$ C、 $\frac{x}{x - 1} = \frac{1}{x - 1}$ D、 $\sqrt{x + 2}$ +3=0

查看试题解析
3. 下列方程组中，属于二元二次方程组的为（）

A、 ${\begin{array}{l} x + y = 0 \\ x - y = 2 \end{array}$ B、 ${\begin{array}{l} \frac{1}{x} + \frac{2}{y} = 3 \\ \frac{2}{x} - \frac{3}{y} = - 4 \end{array}$ C、 ${\begin{array}{l} x + \sqrt{y} = 1 \\ x + y = 1 \end{array}$ D、 ${\begin{array}{l} 3 x = 2 \\ x y = 4 \end{array}$

查看试题解析
4. 一个多边形的内角和是外角和的2倍，这个多边形是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
5. 方程组 ${\begin{matrix} x^{2} - y = 2 \\ 2 x - y = k \end{matrix}$ 有实数解，则k的取值范围是（）

A、 $k \geq 3$ B、 $k = 3$ C、 $k < 3$ D、 $k \leq 3$ ．

查看试题解析
6. 一次函数y=x+1的图象交x轴于点A，交y轴于点B．点C在x轴上，且使得△ABC是等腰三角形，正确点C有（）个．

A、2 B、3 C、4 D、 $5.$

查看试题解析

二、填空题

7. 直线y=-4x-2在y轴上的截距是

查看试题解析
8. 已知一次函数f(x)=- $\frac{1}{2}$ x-2，则f(-2)= ．

查看试题解析
9. 关于x的方程ax=–6有解的条件是．

查看试题解析
10. 方程 $\frac{x}{x - 3}$ =2﹣ $\frac{3}{3 - x}$ 的增根是

查看试题解析
11. 如果一个多边形的每个外角都等于60°，则这个多边形的边数是．

查看试题解析
12. 用换元法解方程 $\frac{3 x}{x^{2} - 1}$ + $\frac{x^{2} - 1}{x}$ =- $\frac{7}{2}$ 时，如果设y= $\frac{x^{2} - 1}{x}$ ，那么原方程可化成关于y的整式方程，这个整式方程是．

查看试题解析
13. 请将方程(x-3) $\sqrt{x - 7}$ =0的解写在后面的横线上：

查看试题解析
14. 在公式 $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ 中，已知正数R、R₁(R≠R₁)，那么R₂= ．

查看试题解析
15. 如果一次函数y=-3x+m-1的图象不经过第一象限，那么m的取值范围是

查看试题解析
16. 已知函数 $y = - 3 x + 7$ ，当 $x > 2$ 时，函数值 $y$ 的取值范围是

查看试题解析
17. 等腰三角形的周长是16(cm)，腰长为x(cm)，底边长为y(cm)，那么y与x之间的函数关系式是(要求写出自变量x的取值范围)．

查看试题解析
18. 把直线y= $\frac{3}{4}$ x+1向右平移个单位可得到直线y= $\frac{3}{4}$ x-2．

查看试题解析

三、解答题

19. 解方程： $\frac{1}{1 - x}$ = $\frac{2}{x + 1}$ -1．

查看试题解析
20. 解方程组： ${\begin{array}{l} 3 x y - y^{2} = 14 ① \\ y - 3 x = 7 ② \end{array}$

查看试题解析
21. 已知一次函数y=(1-2m)x+m+1(m≠ $\frac{1}{2}$ )，函数值y随自变量x值的增大而减小．

(1)、求m的取值范围；

(2)、在平面直角坐标系xOy中，这个函数的图象与x轴的交点M位于x轴的正半轴还是负半轴？请简述理由．

查看试题解析
22. 某校青年老师准备捐款3600元为敬老院的老年人购买一台电脑，这笔钱大家平均承担．实际捐款时又多了2名教师，因为购买电脑所需的总费用不变，于是每人少捐90元．问共有多少人参加捐款？原计划每人捐款多少元？．

查看试题解析
23. 某厂接到一份订单，某运动会开幕式需要720面彩旗，后来由于情况紧急，要求生产总量比原计划增加20%，且必须提前2天完成生产任务，该厂迅速增加人员，实际每天比原计划多生产36面彩旗．请问该厂实际每天生产多少面彩旗？

查看试题解析
24. 一个水槽有进水管和出水管各一个，进水管每分钟进水a升，出水管每分钟出水b升．水槽在开始5分钟内只进水不出水，随后15分钟内既进水又出水，得到时间x(分)与水槽内的水量y(升)之间的函数关系(如图所示)．

(1)、求a、b的值；

(2)、如果在20分钟之后只出水不进水，求这段时间内y关于x的函数解析式及定义域．

查看试题解析
25. 如图，x轴表示一条东西方向的道路，y轴表示一条南北方向的道路，小丽和小明分别从十字路口O点处同时出发，小丽沿着x轴以4千米时的速度由西向东前进，小明沿着y轴以5千米/时的速度由南向北前进．有一颗百年古树位于图中的P点处，古树与x轴、y轴的距离分别是3千米和2千米．

问：

(1)、离开路口后经过多少时间，两人与这棵古树的距离恰好相等？

(2)、离开路口经过多少时间，两人与这颗古树所处的位置恰好在一条直线上？

查看试题解析
26. 已知一次函数 $y = \frac{3}{4} x + 6$ 的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．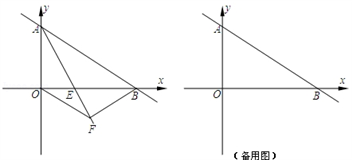

(1)、求点B的坐标；

(2)、求直线AE的表达式；

(3)、过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．

(4)、若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．

查看试题解析