吉林省长春市名校调研（市命题三十)2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-02-19 类型：期中考试

进入出卷网下载

一、单选题

1. 若代数式 $\frac{1}{3 - x}$ 在实数范围内无意义，则实数x的取值范围是（）

A、 $x > 3$ B、 $x = 3$ C、 $x \neq 0$ D、 $x \neq 3$

查看试题解析
2. 下列各点位于平面直角坐标系内第二象限的是（）

A、 $(- 3, 1)$ B、 $(- 3, 0)$ C、 $(3, - 1)$ D、 $(0, 1)$

查看试题解析
3. 如图， $▱ A B C D$ 中， $E G / / F H / / C D$ ，则图中平行四边形有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 关于一次函数 $y = 1 - 2 x$ ，下列说法正确是（）

A、它的图象过点 $(1, - 2)$ B、它的图象经过第一、二、三象限 C、 $y$ 随 $x$ 的增大而增大 D、当 $x > 0$ 时，总有 $y < 1$

查看试题解析
5. 如图，在▱ABCD中，下列结论不一定成立的是（）

A、∠1＝∠2 B、AD＝DC C、∠ADC＝∠CBA D、OA＝OC

查看试题解析
6. 若点 $A (x_{1} ， - 6)$ ， $B (x_{2} ， - 2)$ ， $C (x_{3} ， 2)$ 在反比例函数 $y = \frac{12}{x}$ 的图像上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} < x_{1} < x_{3}$ C、 $x_{2} < x_{3} < x_{1}$ D、 $x_{3} < x_{2} < x_{1}$

查看试题解析
7. 已知 $m + \frac{1}{m} = 3$ ，则 $m^{2} + \frac{1}{m^{2}}$ 的值是（　　）

A、9 B、11 C、7 D、1

查看试题解析
8. 如图， $Rt Δ ABC$ 的顶点 $A$ 的坐标为 $(3 ， 4)$ ，顶点 $B$ 的坐标为 $(- 1 ， 0)$ ，点 $C$ 在 $x$ 轴上，若直线 $y = - 2 x + b$ 与 $Rt Δ ABC$ 的边有交点，则 $b$ 的取值范围为（）

A、 $- 2 < b < 10$ B、 $0 < b < 4$ C、 $- 1 ⩽ b ⩽ 4$ D、 $- 2 ⩽ b ⩽ 10$

查看试题解析

二、填空题

9. 如图，在▱ABCD中，点E、F分别是AB、AD延长线上的点，且∠CDF=62°，则∠CBE=度．

查看试题解析
10. 数据0.00000026用科学记数法表示为 $2.6 \times 10^{n}$ ，则 $n$ 的值是．

查看试题解析
11. 已知在反比例函数y＝ $\frac{1 - k}{x}$ 图象的任一分支上，y都随x的增大而增大，请写出一个符合条件的k的值.

查看试题解析
12. 当 $m$ 满足时，一次函数 $y = - 2 x + 2 m - 5$ 的图象与 $y$ 轴交于负半轴．

查看试题解析
13. 李明读七年级，他家离学校的距离为2000米，如果他上学步行的速度为 $v$ 米/分，从家里到学校的时间为 $t$ 分钟，则 $v$ 与 $t$ 之间的函数关系式为．

查看试题解析
14. 如图，在平面直角坐标系中，四边形OABC是平行四边形，O（0，0），A（1，-2），B（3，1）则C点坐标为．

查看试题解析

三、解答题

15. 先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x}{x^{2} - 1}$ ，其中 $x = 2020$ ．

查看试题解析
16. 已知正比例函数 $y = k x$ 经过点 $A (- 1, 4)$ .

(1)、求正比例函数的表达式；

(2)、将（1）中正比例函数向下平移5个单位长度后得到的函数表达式是．

查看试题解析
17. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $E F$ 过点 $O$ 且与 $A D$ ， $B C$ 分别相交于点 $E$ ， $F$ .求证： $O E = O F$ .

查看试题解析
18. 如图，在平面直角坐标系中，双曲线 $y = \frac{k}{x}$ 过 $▱ A B C D$ 的顶点 $B$ 、 $D$ ，点 $D$ 的坐标为 $(2 ， 1)$ ，点 $A$ 在 $y$ 轴上，且 $A D / / x$ 轴， $S_{▱ A B C D} = 6$ ．

(1)、点 $A$ 的坐标为．

(2)、求双曲线的表达式和点 $B$ 的坐标．

查看试题解析
19. 如图，直线 $y = 2 x + 6$ 与直线 $L ： y = k x + b$ 交于点 $P (- 1 ， m)$

(1)、求 $m$ 的值．

(2)、方程组 ${\begin{array}{l} y = 2 x + 6 \\ y = k x + b \end{array}$ 的解是．

(3)、若直线 $y = a x + n$ 与直线 $y = 2 x + 6$ 平行，且经过点 $(0 ， - 2)$ ，直接写出直线 $y = a x + n$ 的表达式．

查看试题解析
20. 如图，在▱ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于点F.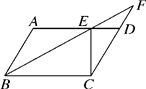

(1)、若∠F＝20°，求∠A的度数；

(2)、若AB＝5，BC＝8，CE⊥AD，求▱ABCD的面积．

查看试题解析
21. 如图，在平面直角坐标系中， $O$ 为坐标原点， $Δ A B O$ 的边 $A B$ 垂直于 $x$ 轴，垂足为 $B$ ，已知 $A B = B O = 4$ ．反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象经过 $A O$ 的中点 $C (2 ， 2)$ ，交 $A B$ 于点 $D$ ．

(1)、求反比例函数 $y = \frac{k}{x}$ 的表达式；

(2)、求经过 $C$ 、 $D$ 两点的直线所对应的函数表达式；

(3)、设点 $E$ 是 $x$ 轴上的动点，请直接写出使 $Δ O C E$ 为直角三角形的点 $E$ 的坐标．

查看试题解析
22. 甲、乙两车分别从A，B两地同时出发相向而行.并以各自的速度匀速行驶，甲车途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象.

(1)、直接写出a，m，n的值；

(2)、求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；

(3)、当两车相距120千米时，乙车行驶了多长时间？

查看试题解析