吉林省吉化六中、吉化三中等四校2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-02-19 类型:期中考试
一、单选题
-
1. 在下列各式中正确是( )A、 =-2 B、 =3 C、 =8 D、 =22. 如图, 于点 , 于点 , 于点 , 则以下四条线段 、 、 和 最短的是( )
 A、 B、 C、 D、3. 若点 的坐标是(2,﹣1),则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 交换下列命题的题设和结论,得到的新命题是假命题的是( )A、两直线平行,内错角相等; B、相等的角是对顶角; C、所有的直角都是相等的; D、若a=b , 则a-1=b-1.5. 将一直角三角板与两边平行的纸条按如图所示的方式放置,有下列结论:(1) ;(2) ;(3) ;(4) .其中正确个数是( )
A、 B、 C、 D、3. 若点 的坐标是(2,﹣1),则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 交换下列命题的题设和结论,得到的新命题是假命题的是( )A、两直线平行,内错角相等; B、相等的角是对顶角; C、所有的直角都是相等的; D、若a=b , 则a-1=b-1.5. 将一直角三角板与两边平行的纸条按如图所示的方式放置,有下列结论:(1) ;(2) ;(3) ;(4) .其中正确个数是( ) A、1个 B、2个 C、3个 D、4个6. 如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
A、1个 B、2个 C、3个 D、4个6. 如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )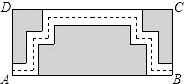 A、100米 B、99米 C、98米 D、74米
A、100米 B、99米 C、98米 D、74米二、填空题
-
7. 图是对顶角量角器,用它测量角度的原理是 .
 8. 在实数:﹣ ,3.14159, , ,π,1.010010001…(每相邻两个1之间的0依次多1) 中,无理数有个.9. 若点 ( , )在 轴上,则点 的坐标为.10. 已知a、b为两个连续的整数,且 , 则a+b= .
8. 在实数:﹣ ,3.14159, , ,π,1.010010001…(每相邻两个1之间的0依次多1) 中,无理数有个.9. 若点 ( , )在 轴上,则点 的坐标为.10. 已知a、b为两个连续的整数,且 , 则a+b= .
11. 已知点 到 轴的距离是2,到 轴的距离是5,则满足条件的 点坐标有个.12. 如图, ∥ ∥ ,当 , 时, . 13. 对于两个有理数a,b,定义一种新运算如下: ,如: ,那么 .
13. 对于两个有理数a,b,定义一种新运算如下: ,如: ,那么 .三、解答题
-
14. 计算:15.(1)、(2)、16. 如图,已知∠1=∠2,∠3+∠4=180°.求证:AB∥EF
 17. 已知 ,且 是负数,求 的值.18. 完成下面的证明
17. 已知 ,且 是负数,求 的值.18. 完成下面的证明如图,FG//CD , ∠1=∠3,∠B=50°,求∠BDE的度数.

解:∵FG//CD (已知)
∴∠2=()
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//()
∴∠B+=180°()
又∵∠B=50°
∴∠BDE=.
19. 已知 的平方根是±1, 的立方根是3,求 的算术平方根.20. 在平面直角坐标系中,一蚂蚁从原点 出发,按向上、向右、向下、向右的方向依次不断移动每次移动1个单位,其行走路线如图所示. (1)、填写下列各点的坐标: , ;(2)、写出点 的坐标( 为正整数);(3)、蚂蚁从点 到点 的移动方向 .21. 已知点 (1,0)、 (0,2),点 在 轴上,且△PAB的面积为5.(1)、满足点 的坐标有个;(2)、求出满足点 的坐标.22. 如图,已知 , , , 经过平移得到的 , 中任意一点 平移后的对应点为 .
(1)、填写下列各点的坐标: , ;(2)、写出点 的坐标( 为正整数);(3)、蚂蚁从点 到点 的移动方向 .21. 已知点 (1,0)、 (0,2),点 在 轴上,且△PAB的面积为5.(1)、满足点 的坐标有个;(2)、求出满足点 的坐标.22. 如图,已知 , , , 经过平移得到的 , 中任意一点 平移后的对应点为 .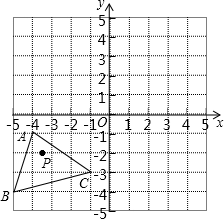 (1)、请在图中作出 ;(2)、写出点 、 、 的坐标;(3)、求 的面积.23. 如图, 和 的平分线交于点E,BE的延长线交CD于点F,且 ,求证:
(1)、请在图中作出 ;(2)、写出点 、 、 的坐标;(3)、求 的面积.23. 如图, 和 的平分线交于点E,BE的延长线交CD于点F,且 ,求证: (1)、AB∥CD;(2)、猜想∠2与∠3的关系并证明.24. 已知一个角的两边与另一个角的两边分别平行,请结合图形探索这两个角之间的关系,并说明理由。(1)、如图①, ∥ , ∥ , 猜想 与 的关系,并说明理由;
(1)、AB∥CD;(2)、猜想∠2与∠3的关系并证明.24. 已知一个角的两边与另一个角的两边分别平行,请结合图形探索这两个角之间的关系,并说明理由。(1)、如图①, ∥ , ∥ , 猜想 与 的关系,并说明理由; (2)、如图②, ∥ , ∥ , 猜想 与 的关系,并说明理由;
(2)、如图②, ∥ , ∥ , 猜想 与 的关系,并说明理由; (3)、由(1)(2),我们可以得出结论:一个角的两边与另一个角的两边分别平行,那么这两个角;(4)、应用:两个角的两边分别平行,且一个角比另一个角的3倍少60°,求出这两个角的度数分别是多少度?25. 如图所示, 、点 ,将 沿 轴负方向平移3个单位,平移后得到图形为 ,且点 的坐标为 .
(3)、由(1)(2),我们可以得出结论:一个角的两边与另一个角的两边分别平行,那么这两个角;(4)、应用:两个角的两边分别平行,且一个角比另一个角的3倍少60°,求出这两个角的度数分别是多少度?25. 如图所示, 、点 ,将 沿 轴负方向平移3个单位,平移后得到图形为 ,且点 的坐标为 . (1)、直接写出点D的坐标 , 点 的坐标;
(1)、直接写出点D的坐标 , 点 的坐标;
(2)、线段 与 的位置关系;(3)、在四边形 中,点 从点 出发,沿“ → ”移动.若点 的速度为每秒1个单位长度,运动时间为 秒,直接写出点P在运动过程中的坐标(用含t的式子表示);(4)、当点 在线段 上时,设 , , ,试问 , , 之间的数量关系能否确定?若能,请用含 , 的式子表示 ,写出过程;若不能,说明理由.