广东省中山市城东教学共进联盟2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-02-19 类型:期中考试
一、单选题
-
1. 如图所示, 和 是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 2. 121的平方根是( )A、 B、11 C、 D、3. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列说法正确是( )A、同位角相等 B、过一点有且只有一条直线与已知直线平行 C、正数、负数统称实数 D、在同一平面内,过一点有且只有一条直线与已知直线垂直5. 估计 的值( )A、在3到4之间 B、在4到5之间 C、在5到6之间 D、在6到7之间6. 在3.14、 、 、0、 、 、0.2020020002这七个数中,无理数有( )A、1个 B、2个 C、3个 D、4个7. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、8. 如图所示,点 在 的延长线上,下列条件中能判断 的是( )
2. 121的平方根是( )A、 B、11 C、 D、3. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列说法正确是( )A、同位角相等 B、过一点有且只有一条直线与已知直线平行 C、正数、负数统称实数 D、在同一平面内,过一点有且只有一条直线与已知直线垂直5. 估计 的值( )A、在3到4之间 B、在4到5之间 C、在5到6之间 D、在6到7之间6. 在3.14、 、 、0、 、 、0.2020020002这七个数中,无理数有( )A、1个 B、2个 C、3个 D、4个7. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、8. 如图所示,点 在 的延长线上,下列条件中能判断 的是( ) A、 B、 C、 D、9. 如图,直线 , 相交于点 , ,垂直为点 , ,则 ( )
A、 B、 C、 D、9. 如图,直线 , 相交于点 , ,垂直为点 , ,则 ( ) A、40° B、130° C、50° D、140°10. 如图,将直角 沿着点 到点 的方向平移到 的位置, , ,平移距离为6,则阴影部分面积为( )
A、40° B、130° C、50° D、140°10. 如图,将直角 沿着点 到点 的方向平移到 的位置, , ,平移距离为6,则阴影部分面积为( ) A、48 B、30 C、38 D、50
A、48 B、30 C、38 D、50二、填空题
-
11. 的立方根为12. 点 到 轴的距离为 , 到 轴的距离为.13. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠1=40°时,那么∠2的度数是 .
 14. 已知点 坐标为 在 轴上,写出 点坐标.15. 已知 , 则16. 如图, 平分 平分 ,则 .
14. 已知点 坐标为 在 轴上,写出 点坐标.15. 已知 , 则16. 如图, 平分 平分 ,则 .
三、解答题
-
17. 计算:18. 如图,已知表示棋子“炮”和“車”的点的坐标分别为 、 ,
 (1)、请你根据题目条件,在图上画出平面直角坐标系.(2)、分别写出“马”和“帅”的坐标.(3)、将“車”向上平移1个单位,再向右平移5个单位后的坐标.19. 一个长方形的面积为 ,它的长和宽之比为 ,求这个长方形的长和宽.20. 已知一个正数 的平方根是 与 , 立方根是2,求 的平方根.21. 如图,在平面直角坐标系 中, 的三个顶点的坐标分别是 , , .将 向上平移5个单位长度,再向右平移8个单位长度,得到 .
(1)、请你根据题目条件,在图上画出平面直角坐标系.(2)、分别写出“马”和“帅”的坐标.(3)、将“車”向上平移1个单位,再向右平移5个单位后的坐标.19. 一个长方形的面积为 ,它的长和宽之比为 ,求这个长方形的长和宽.20. 已知一个正数 的平方根是 与 , 立方根是2,求 的平方根.21. 如图,在平面直角坐标系 中, 的三个顶点的坐标分别是 , , .将 向上平移5个单位长度,再向右平移8个单位长度,得到 . (1)、在平面直角坐标系 中画出 并写出 的坐标.(2)、求 的面积.(3)、 为三角形 中任意一点,则平移后对应点 的坐标为.22. 已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
(1)、在平面直角坐标系 中画出 并写出 的坐标.(2)、求 的面积.(3)、 为三角形 中任意一点,则平移后对应点 的坐标为.22. 已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.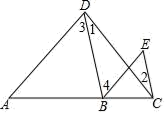 23. 如图,已知 , , 平分 , .
23. 如图,已知 , , 平分 , . (1)、 ,求 和 的度数.(2)、判断等式 是否成立,并说明理由.24. 如图,在平面直角坐标系中,已知 , ,其中 , 满足 ,点 为第三象限内一点.
(1)、 ,求 和 的度数.(2)、判断等式 是否成立,并说明理由.24. 如图,在平面直角坐标系中,已知 , ,其中 , 满足 ,点 为第三象限内一点. (1)、若 到坐标轴的距离相等, ,且 ,求 点坐标(2)、若 为 ,请用含 的式子表示 的面积.(3)、在(2)条件下,当 时,在 轴上有点 ,使得 的面积是 的面积的2倍,请求出点 的坐标.25. 已知, , ,试回答下列问题:(1)、如图1所示,求证: .
(1)、若 到坐标轴的距离相等, ,且 ,求 点坐标(2)、若 为 ,请用含 的式子表示 的面积.(3)、在(2)条件下,当 时,在 轴上有点 ,使得 的面积是 的面积的2倍,请求出点 的坐标.25. 已知, , ,试回答下列问题:(1)、如图1所示,求证: . (2)、如图2,若点 、 在 上,且满足 ,并且 平分 .求 度.
(2)、如图2,若点 、 在 上,且满足 ,并且 平分 .求 度. (3)、在(2)的条件下,若平行移动 ,如图3,那么 的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(3)、在(2)的条件下,若平行移动 ,如图3,那么 的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值. (4)、在(2)的条件下,如果平行移动 的过程中,若使 ,求 度数.
(4)、在(2)的条件下,如果平行移动 的过程中,若使 ,求 度数.