广东省肇庆市封开县2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期：2020-02-19 类型：期中考试
一、单选题
-
1.
如图，在所标识的角中，互为对顶角的两个角是（ ）
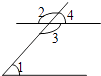A、∠2和∠3 B、∠1和∠3 C、∠1和∠4 D、∠1和∠22. 下列各式中正确是（ ）A、 B、 C、 D、3. 如图，AB∥ED，AG平分∠BAC，∠ECF=70°，则∠FAG的度数是（ ）
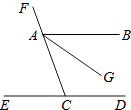A、155° B、145° C、110° D、35°4. 下列结论正确是（ ）A、无限小数都是无理数 B、无理数都是无限小数 C、带根号的数都是无理数 D、实数包括正实数、负实数5. 如图，下列四组条件中，能判断AB∥CD的是（ ）
A、∠1＝∠2 B、∠BAD＝∠BCD C、∠ABC＝∠ADC，∠3＝∠4 D、∠BAD＋∠ABC＝180°6. 在平面直角坐标系中，已知点P（﹣2，3），则点P在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如果实数a= ，且a在数轴上对应点的位置如图所示，其中正确是（ ）A、
B、
C、
D、
8. 如图所示，AB∥CD，∠DEF=120°，则∠B的度数为（ ）
A、120° B、60° C、150° D、30°9. 在平面直角坐标系中，已知点A（﹣4，﹣1）和B（﹣1，4），平移线段AB得到线段A1B1 ， 使平移后点A1的坐标为（2，2），则平移后点B1坐标是（ ）A、（﹣3，1） B、（﹣3，7） C、（1，1） D、（5，7）10. 在实数范围内，下列判断正确是（ ）A、若 ，则m=n B、若 ，则a＞b C、若 ，则a=b D、若 ，则a=b二、填空题
-
11. 如图，∠1＝15°，∠AOC＝90°.若点B，O，D在同一条直线上，则∠2＝ ．
12.如图所示，在铁路旁边有一李庄，现要建一火车站，为了使李庄人乘火车最方便（即距离最近），请你在铁路旁选一点来建火车站（位置已选好），说明理由： ．
13. 是一个（填“正或负”）实数，它的相反数是、绝对值是 ．14. 把命题“同旁内角互补，两直线平行”改写成“如果……，那么……”的形式： ．15. 在平面直角坐标系中，点A（2t﹣1，3t+2）在y轴上，则t的值为 ．16. 通过估算写出大于 但小于 的整数 ．三、解答题
-
17. 计算：(1)、 ；(2)、 ．18. 如图，直线AB与CD相交于点O，EO⊥CD于点O，OF平分∠AOD，且∠BOE＝50°.求∠COF的度数．
19. 如图，已知△ABC在平面直角坐标系中的位置如图所示，
(1)、写出△ABC三个顶点的坐标；(2)、求出△ABC的面积；(3)、在图中画出把△ABC先向左平移5个单位，再向上平移2个单位后所得的△A′B′C′，并写出各顶点坐标．20. 已知，如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．
请完成以下证明过程：
证明：∵AB∥CD(已知)
∴∠AEF=∠EFD（）
∵EG平分∠AEF，FH平分∠EFD（）
∴∠＝ ∠AEF，∠= ∠EFD（）
∴∠=∠(等量代换)
∴EG∥FH（）．
21. 如图，已知E是AB上的点，AD∥BC ， AD平分∠EAC ， 试判定∠B与∠C的大小关系，并说明理由．
22. 求下列各式中的x ．(1)、 x2﹣121＝0(2)、(x﹣5)3+8＝023. 已知一个数x的两个平方根分别是3a+2和a+14，求a和x的值．24. 如图，已知四边形ABCD中，∠D＝100°，AC平分∠BCD，且∠ACB＝40°，∠BAC＝70°.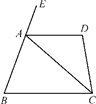
(1)、AD与BC平行吗？试写出推理过程；(2)、求∠DAC和∠EAD的度数.25. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足 +|b﹣6|=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动．
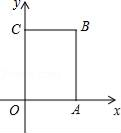(1)、a= ， b= ， 点B的坐标为；(2)、当点P移动4秒时，请指出点P的位置，并求出点P的坐标；(3)、在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．