山东省聊城市莘县2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期:2020-02-18 类型:期末考试
一、选择题(本题共12小题。每题3分,满分36分)
-
1. tan30°的值等于( )A、 B、 C、 D、2. 如图,A、D是⊙O上的两个点,若∠ADC=33°,则∠ACO的大小为
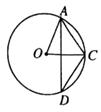 A、57° B、66° C、67° D、44°3. 下列诗句所描述的事件中,是不可能事件的是( )A、黄河人海流 B、锄禾日当午 C、大漠孤烟直 D、手可摘星辰4. 以3、4为两边的三角形的第三边长是方程x2-13x+40=0的根,则这个三角形的周长为( )A、15或12 B、12 C、15 D、以上都不对5. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( )
A、57° B、66° C、67° D、44°3. 下列诗句所描述的事件中,是不可能事件的是( )A、黄河人海流 B、锄禾日当午 C、大漠孤烟直 D、手可摘星辰4. 以3、4为两边的三角形的第三边长是方程x2-13x+40=0的根,则这个三角形的周长为( )A、15或12 B、12 C、15 D、以上都不对5. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( ) A、 B、 C、 D、6. 右图是以△ABC的边AB为直径的半圆O,点c恰好在半圆上,过C作CD上AB交AB于D,已知cos∠ACD= ,BC=4,则AC的长为( )
A、 B、 C、 D、6. 右图是以△ABC的边AB为直径的半圆O,点c恰好在半圆上,过C作CD上AB交AB于D,已知cos∠ACD= ,BC=4,则AC的长为( )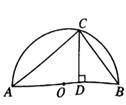 A、1 B、 C、3 D、7. 在反比例函数y= 的图象中,阴影部分的面积不等于4的是( )A、
A、1 B、 C、3 D、7. 在反比例函数y= 的图象中,阴影部分的面积不等于4的是( )A、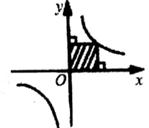 B、
B、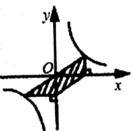 C、
C、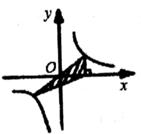 D、
D、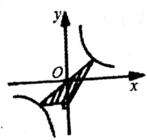 8. 如图,矩A形OABC的顶点O是B坐标原点,边OA在x轴上,边OC在y轴上若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的 ,则点B1的坐标是( )
8. 如图,矩A形OABC的顶点O是B坐标原点,边OA在x轴上,边OC在y轴上若矩形OA1B1C1与矩形OABC关于点O位似,且矩形OA1B1C1的面积等于矩形OABC面积的 ,则点B1的坐标是( )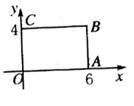 A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)9. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)9. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )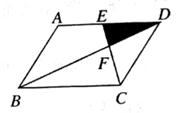 A、11S B、10S C、9S D、8S10. 已知二次函数y=-2(x-a)2-b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是( )
A、11S B、10S C、9S D、8S10. 已知二次函数y=-2(x-a)2-b的图象如图所示,则反比例函数y= 与一次函数y=ax+b的图象可能是( ) A、
A、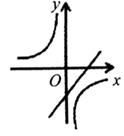 B、
B、 C、
C、 D、
D、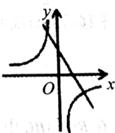 11. 如图,点O为正五边形BCDE外接圆的圆心,五边形ABCDE的对角线分别相交于点P,Q,R,M,N.若顶角等于36°的等腰三角形叫做黄金三角形,那么图中共有( )个黄金三角形.
11. 如图,点O为正五边形BCDE外接圆的圆心,五边形ABCDE的对角线分别相交于点P,Q,R,M,N.若顶角等于36°的等腰三角形叫做黄金三角形,那么图中共有( )个黄金三角形.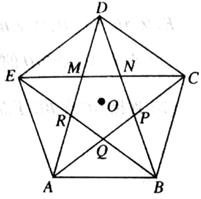 A、5 B、10 C、15 D、2012. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:
A、5 B、10 C、15 D、2012. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论: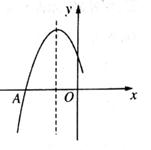
①abc>0;②4a+b=0;③若点B(3,y1)、C(-4,y2)为函数图象上的两点,则y1>y2;④关于x的方程ax2+bx+c+2=0一定有两个不相等的实数根其中,正确结论的个数是( )
A、4 B、3 C、2 D、1二、填空题(本题共5小题,每题3分,满分15分)
-
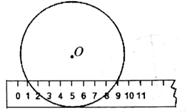
13. 计算sin60°tan60°- cos45°cos60°的结果为 。14. 已知关于x的方程(k-1)x2-2kx+k-3=0有两个不相等的实数根,则k的取值范围是。15. 当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为cm。
 16. 如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 。
16. 如图,圆锥的表面展开图由一扇形和一个圆组成,已知圆的面积为100π,扇形的圆心角为120°,这个扇形的面积为 。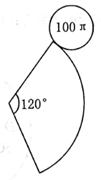 17. 如图在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 的长为。
17. 如图在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1 , 交x轴正半轴于点O2 , 以O2为圆心,O2O为半径画圆,交直线l于点P2 , 交x轴正半轴于点O3 , 以O3为圆心,O3O为半径画圆,交直线l于点P3 , 交x轴正半轴于点O4;…按此做法进行下去,其中 的长为。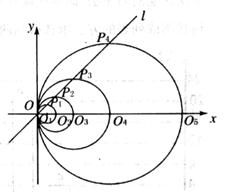
三、解答题(本题共8小题,共69分)
-
18. 解方程(1)、2x2+1=3x(用配方法)(2)、(x-2)2-3(x-2)-4=0(3)、 -3tan30°+(π-4)0+( )-119. 全面二孩政策于2016年1月1日正式实施,聊城市某中学对八年级部分学生进行了随机问卷调查,其中一个问题“你爸妈如果给你添一个弟弟(或妹妹),你的态度是什么?”共有如下四个选项(要求仅选择一个选项):
A.非常愿意 B.愿意 C.不愿意 D.无所谓
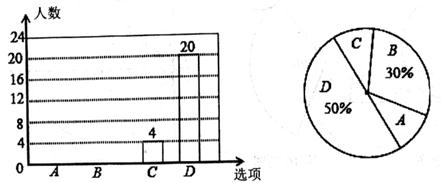
如图是根据调查结果绘制的两幅不完整的统计图,请结合图中信息解答以下问题:
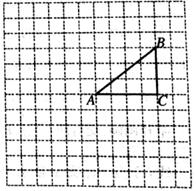
(1)、试问本次问卷调查一共调查了多少名学生?并补全条形统计图;(2)、若该年级共有450名学生,请你估计全年级可能有多少名学生支持(即态度为“非常愿意”和“愿意”)爸妈给自己添一个弟弟(或妹妹)?(3)、在年级活动课上,老师决定从本次调查回答“不愿意”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“不愿意”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率。20. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点△ABC的三个顶点A,B,C都在格点上将△ABC绕点A顺时针方向旋转90°得到△AB'C'。
 (1)、在正方形网格中,画出△AB'C';(2)、计算线段AB在旋转到AB的过程中所扫过区域的面积(结果保留π)21. 如图,点A是我市某小学,在位于学校南偏西15°方向距离120米的C点处有一消防车某一时刻消防车突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即沿路线CF赶往救火。已知消防车的警报声传播半径为110米,问消防车的警报声对学校是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对学校的影响时间为几秒?( ≈3.6,结果精确到1秒)
(1)、在正方形网格中,画出△AB'C';(2)、计算线段AB在旋转到AB的过程中所扫过区域的面积(结果保留π)21. 如图,点A是我市某小学,在位于学校南偏西15°方向距离120米的C点处有一消防车某一时刻消防车突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即沿路线CF赶往救火。已知消防车的警报声传播半径为110米,问消防车的警报声对学校是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对学校的影响时间为几秒?( ≈3.6,结果精确到1秒)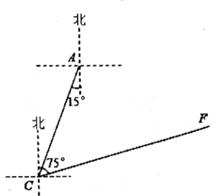 22. 如图,在直角坐标系中,直线y= x与反比例函数y= 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3。
22. 如图,在直角坐标系中,直线y= x与反比例函数y= 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3。 (1)、求反比例函数的表达式;(2)、将直线y= x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式。23. 如图,在R△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE。
(1)、求反比例函数的表达式;(2)、将直线y= x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式。23. 如图,在R△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE。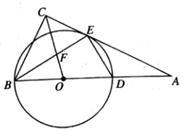 (1)、求证:AC是⊙O的切线;(2)、连接OC交BE于点F,若 ,求 的值。24. 某化工材料经销公司购进一种化工原料若干千克价格为每千克30元物价部门规定其销售单价不高于每千克60元,不低于每千克30元经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100在销售过程中,每天还要支付其他费用450元。(1)、求出y与x的函数关系式,并写出自变量x的取值范围。(2)、求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。(3)、当销售单价为多少元时,该公司日获利最大?最大获利是多少元?25. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B。
(1)、求证:AC是⊙O的切线;(2)、连接OC交BE于点F,若 ,求 的值。24. 某化工材料经销公司购进一种化工原料若干千克价格为每千克30元物价部门规定其销售单价不高于每千克60元,不低于每千克30元经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100在销售过程中,每天还要支付其他费用450元。(1)、求出y与x的函数关系式,并写出自变量x的取值范围。(2)、求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。(3)、当销售单价为多少元时,该公司日获利最大?最大获利是多少元?25. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B。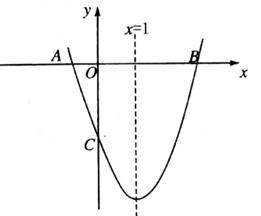 (1)、求这条抛物线所对应的函数关系式;(2)、在抛物线的对称轴x=1上求一点M使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;(3)、设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标。
(1)、求这条抛物线所对应的函数关系式;(2)、在抛物线的对称轴x=1上求一点M使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;(3)、设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标。