河北省衡水市景县2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期：2020-02-18 类型：期末考试
一、选择(每小题3分，共48分)
-
1. 若关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0，则a的值是（ ）A、1 B、-1 C、1或-1 D、2. 下列函数中，是二次函数的有（ ）个
y=(x-3)2-1 y=1- x2 y= (x+2)(x-2) y=(x-1)2-x2
A、1 B、2 C、3 D、43. 下面的图形中，是轴对称图形但不是中心对称图形的是（ ）A、
B、
C、
D、
4. 用直接开平方法解方程(x-3)2=8，得方程的根为（ ）A、x=3+2 B、x=3-2 C、x1=3+2 ，x2=3-2 D、x1=3+2 ，x2=3-25. 如图，AB切⊙O于点B，OA=2 ，AB=3，弦BC∥OA，则劣弧BC的长度为（ ）
A、 B、 C、π D、6. 如图，若用圆心角为120°，半径为9的扇形围成一个圆锥侧面(接缝忽略不计)，则这个锥的底面直径是（ ）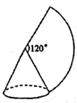
A、6 B、3 C、9 D、127. 三角形的外心具有的性质是（ ）A、到三边距离相等 B、到三个顶点距离相等 C、外心在三角形外 D、外心在三角形内8. 现有一水塔，水塔内装有水40m3 ， 如果每小时从排水管中放水x(m3)，则要经过y(h)就可以把水放完该函数的图象大致应是下图中的（ ）A、
B、
C、
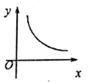D、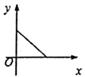
9. △ABC中，AB=AC=5，BC=8，点P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（ ）
A、4.8 B、4.8或3.8 C、3.8 D、510. 平面直角坐标系中，已知点O(0，0)、A(0，2)、B(1，0)，点P是反比例函数y= 象上的一个动点，过点P作PQ⊥x轴，垂足为点Q若以点O、P、Q为顶点的三角形与△OAB相似，则相应的点P共有（ ）A、1个 B、2个 C、3个 D、4个11. 如图，点A是反比例函数y=(x<0)的图象上的一点，过点A作平行四边形ABCD，使点B、C在x轴上，点D在y轴上已知平行四边形ABCD的面积为6，则k的值为（ ）
A、6 B、-6 C、3 D、-312. 如图，将Rt△ABC绕点A逆时针旋转40°，得到Rt△AB'C'，点C恰好落在斜边AB上，连接BB’，则∠BB’C’=（ ）度。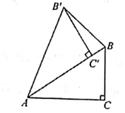
A、25 B、20 C、30 D、1513. 如图，为了测量某棵树的高度，小明用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点此时，竹竿与这一点距离相距6m，与树相距15m，则树的高度为（ ）m．
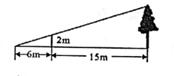A、6 B、9 C、7 D、414. 图1是一个地铁站入口的双翼闸机如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC=BD=54cm，且与闸机侧立面夹角∠PCA=∠BDQ=30°，当双翼收起时，可以通过闸机的物体的最大宽度为（ ）
A、(54 +10)cm B、( +10)cm C、64cm D、54cm15. 已知二次函数y=ax2+bx+c(a≠0)的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=-1；③当x=1时，y=2a；④am2+bm+a>0(m≠-1)其中正确的个数是（ ）
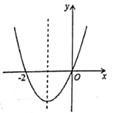A、1 B、2 C、3 D、416. 如图示，若△ABC内一点P满足∠PAC=∠PBA=∠PCB，则点P为△ABC的布洛卡点三角形的布洛卡点( Brocard point)是法国数学家和数学教育家克洛尔(A．L． Crelle.1780-1855)于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡( Brocard1845-1922)重新发现，并用他的名字命名问题：已知在等腰直角三角形DEF中，∠EDF=90°，若点Q为△DEF的布洛卡点，DQ=1，则EQ+FQ=（ ）
A、5 B、4 C、3+ D、2+二、填空(每空3分，共12分)
-
17. 一个反比例函数y= (k≠0)的图象经过点P(-2，-1)，则该反比例函数的解析式是。18. 关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根，则k的范围为。19. 已知矩形ABCD的边AB=3cm，AD=4cm，若以点A为圆心，2 cm长为半径作⊙A，则点D与⊙A的位置关系。若以点A为圆心作⊙A，使得B、C、D三点中有且只有一点在圆外，则⊙A的半径r的取值范围是。
三、解答
-
20. 计算(1)、cos45°-2sin30°+(-2)°(2)、2tan30°-|1- |+(2017- )°+21. 已知分式 ，若n满足一元二次方程n2+n-2=0，先化简原分式，再求值。22. 为了解今年初三学生的数学学习情况，某校在第一轮模拟测试后，对初三全体同学的数学成绩作了统计分析，绘制如下图表：请结合图表所给出的信息解答系列问题：
成绩
绩效
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
0
(1)、该校初三学生共有多少人?(2)、求表中a，b，c的值，并补全条形统计图(3)、初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍求恰好选中甲、乙两位同学的概率．23. 如图，正方形网格中，△ABC为格点三角形(顶点都是格点)，将△ABC绕点A按逆时针方向旋转90°，得到△AB1C1
(1)、在正方形网格中，作出△AB1C1；(2)、设网格小正方形的边长为1，求旋转过程中动点B所经过的路径长24. 某超市购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出500个，根据销售经验，售价每提高1元，销售量相应减少10个，如果超市将篮球售价定为x元(x>50)，每月销售这种篮球获利y元(1)、求y与x之间的函数关系式；(2)、超市计划下月销售这种篮球获利8000元，又要吸引更多的顾客，那么这种篮球的售价为多少元?25. 如图，AB是⊙O的弦，半径OE⊥AB，P为AB的延长线上一点，PC与⊙O相切于点C，CE与AB交于点F．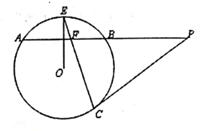
(1)、求证：PC=PF；(2)、连接OB，BC，若OB∥PC，BC=3 ，tanP= ，求FB的长。26. 如图，已知抛物线y=ax2+bx+c与x轴的一个交点为A(3，0)，与y轴的交点为点B(0，3)，其顶点为C对称轴为x=1，
(1)、求抛物线的解析式；(2)、已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；(3)、将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S．