河北省衡水市景县2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-02-18 类型：期末考试

进入出卷网下载

一、一、选择题(本大题共12小题，每小题3分，共36分)

1. 在式子 $\frac{1}{a} ， \frac{20 y}{π} ， \frac{3 a b^{3} c}{4} ， \frac{5}{6 + x} ， \frac{x}{7} + \frac{y}{8} ， 9 x + \frac{10}{y}$ 中，分式的个数有（　　）

A、2 B、3 C、4 D、5

查看试题解析
2. 一个三角形的两边长分别为3cm和8cm，则此三角形第三边长可能是（）

A、3cm B、5cm C、7cm D、11cm

查看试题解析
3. 下列四个图形是四款车的标志，其中轴对称图形有几个（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列计算正确的是（）

A、(a²)³=a⁵ B、（15x²y-10xy²）÷5xy=3x-2y C、10ab³÷(-5ab)=-2ab² D、a^-2b³·(a²b-1)^-2= $\frac{b^{6}}{a^{6}}$

查看试题解析
5. 我国的纸伞工艺十分巧妙。如图，伞不论张开还是缩拢，伞柄AP始终平分同一平面内所成的角∠BAC，从而保证伞圈D能沿着伞柄滑动。为了证明这个结论，我们的依据是（）

A、SSS B、SAS C、AAS D、ASA

查看试题解析
6. 下列各多项式从左到右变形是因式分解，并分解正确的是（）

A、(a-b)³-b(b-a)²=(b-a)²(a-2b) B、(x+2)(x+3)=x²+5x+6 C、4a²-9b²=(4a-9b)(4a+9b) D、m²-n²+2=(m+n)(m-n)+2

查看试题解析
7. 解分式方程 $\frac{2}{x - 1} + \frac{x + 2}{1 - x} = 3$ 时，去分母后变形正确的是（）

A、2+(x+2)=3(x-1) B、2-x+2=3(x-1) C、2-(x+2)=3 D、2-(x+2)=3（x-1）

查看试题解析
8.
如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）

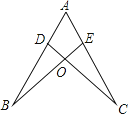A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD

查看试题解析
9. 根据图①的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a²+3ab+b² ，那么根据图②的面积可以说明少项式的乘法运算是（）

A、(a+3b)(a+b)=a²+4ab+3b² B、(a+3b)(a+b)=a²+3b² C、(b+3a)(b+a)=b²+4ab+3a² D、(a+3b)(a-b)=a²+2ab-3b²

查看试题解析
10. 如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D，如果CE=12，则ED的长为（）

A、3 B、4 C、5 D、6

查看试题解析
11. 某部门组织调运一批物资，一运送物资车开往距离出发地180千米的目的地，出发第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40分钟到达目的地设原计划速度为x千米/小时，则方程可列为（）

A、 $\frac{180}{x} + \frac{40}{60} = \frac{180}{1.5 x}$ B、 $\frac{180}{x} - \frac{40}{60} = \frac{180 - x}{1.5 x}$ C、 $\frac{180 - x}{1.5 x} + 1 = \frac{180}{x} - \frac{40}{60}$ D、 $\frac{180 - x}{1.5 x} + 1 = \frac{180}{x} + \frac{40}{60}$

查看试题解析
12. 如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN则在点M运动过程中，线段HN长度的最小值是（）

A、12 B、6 C、3 D、1

查看试题解析

二、填空题(本大题共6小题，每小题3分，共18分)

13. 若式子 $\frac{x^{2} - 1}{(x - 1) (x + 2)}$ 的值为零，则x的值为．

查看试题解析
14. 水由氢原子和氧原子组成，其中氢原子的直径约为0.0000000001，用科学记数法表示为米。

查看试题解析
15. 因式分解：ab²-a=。

查看试题解析
16. 等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是．

查看试题解析
17. 若多项式9x²-2(m+1)xy+4y²是一个完全平方式，则m=。

查看试题解析
18. 如图1，△ABC中，AD是∠BAC的平分线，若AB=AC+CD，那么∠ACB与∠ABC有怎样的∠数量关系个?小明通过观察分析，形成了如下解题思路：

如图2，延长AC到E，使CE=CD，连接DE由AB=AC+CD，可得AE=AB．又因为AD是∠BAC的平分线，可得△ABD≌△AED，进一步分析就可以得到∠ACB与∠ABC的数量关系。

(1)、判定△ABD与△AED全等的依据是；

(2)、∠ACB与∠ABC的数量关系为：。

查看试题解析

三、解答题(本大题有8个小题，共66分。)

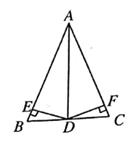
19. 用简便方法计算：

(1)、100²-200×99+99²

(2)、2018×2020-2019²

查看试题解析
20. 解下列分式方程：

(1)、 $\frac{2}{x - 1} - \frac{3}{x + 1} = \frac{x + 3}{x^{2} - 1}$

(2)、 $\frac{x}{x - 1} = \frac{3}{2 x - 2} - 2$

查看试题解析
21. 先化简再求值： $(\frac{4 a - 4}{a - 2} - a - 2) \div \frac{a - 4}{a^{2} - 4 a + a}$ 其中a与2，3构成△ABC的三边，且a为整数．

查看试题解析
22. 如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF。求证：AD是△ABC的角平分线。

查看试题解析
23. 对于多项式x³-5x²+x+10，我们把x=2代入此多项式，发现x=2能使多项式x³-5x²+x+10的值为0，由此可以断定多项式x³-5x²+x+10中有因式(x-2)，(注：把x=a代入多项式，能使多项式的值为0，则多项式一定含有因式(x-a)，于是我们可以把多项式写成：x³-5x²+x+10=(x-2)(x2+mx+n)，分别求出m、n后再代入x³-5x²+x+10=(x-2)(x²+mx+n)，就可以把多项式x³-5x²+x+10因式分解

(1)、求式子中m、n的值；

(2)、以上这种因式分解的方法叫“试根法”，用“试根法”分解多项式x³+5x²+8x+4

查看试题解析
24. 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动(D不与B、C重合)，连接AD，作∠ADE=40°，DE与AC交于E。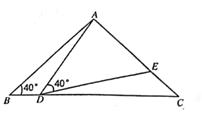

(1)、当∠BDA=115°时，∠BAD=°，∠DEC=°，当点D从B向C运动时，∠BDA逐渐变(填“大”或“小”)；

(2)、当DC等于多少时，△ABD与△DCE全等?请说明理由；

(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗?若可以，请直接写出∠BDA的度数；若不可以，请说明理由。

查看试题解析
25. 某地在城区美化工程招标时，有甲、乙两个工程队投标，经测算，获得以下信息：
信息1：乙队单独完成这项工程需要60天；

信息2：若先由甲、乙两队合做16天，剩下的工程再由乙队单独做20天可以完成；

信息3：甲队施工一天需付工程款35万元，乙队施工一天需付工程款2万元

根据以上信息，解答下列问题

(1)、甲队单独完成这项工程需要多少天?

(2)、若该工程计划在50天内完成在不超过计划天数的前提下，是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?

查看试题解析
26. 如图，在△ABC中，∠ACB=90°，∠ABC=30°，△CDE是等边三角形，点D在边AB上。

(1)、如图1，当点E在边BC上时，求证DE=EB；

(2)、如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

(3)、如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG=5CG，BH=3求CG的长。

查看试题解析

河北省衡水市景县2019-2020学年八年级上学期数学期末考试试卷

一、一 、选择题(本大题共12小题，每小题3分，共36分)

二、填空题(本大题共6小题，每小题3分，共18分)

三、解答题(本大题有8个小题，共66分。)

一、一、选择题(本大题共12小题，每小题3分，共36分)