初中数学浙教版九年级下册2.1 直线和圆的位置关系(3) 同步训练
试卷更新日期:2020-02-18 类型:同步测试
一、基础夯实
-
1. 如图,已知 是 的内接三角形, 是 的切线,点 为切点, ,则 的度数是( )
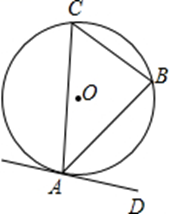 A、30° B、45° C、60° D、120°2. 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,若∠C=40°,则∠B的度数为( )
A、30° B、45° C、60° D、120°2. 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,若∠C=40°,则∠B的度数为( ) A、60° B、50° C、40° D、30°.3. 如图, 是⊙O 的直径, 是⊙O 的切线, 为切点, ,则 等于( )
A、60° B、50° C、40° D、30°.3. 如图, 是⊙O 的直径, 是⊙O 的切线, 为切点, ,则 等于( )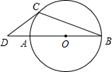 A、25° B、50° C、30° D、40°4. 如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36°,则∠B等于( )。
A、25° B、50° C、30° D、40°4. 如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=36°,则∠B等于( )。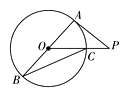 A、27° B、32° C、36° D、54°5. 如图为 和一圆的重叠情形,此圆与直线 相切于 点,且与 交于另一点 .若 , ,则 的度数为何( )
A、27° B、32° C、36° D、54°5. 如图为 和一圆的重叠情形,此圆与直线 相切于 点,且与 交于另一点 .若 , ,则 的度数为何( )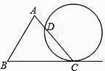 A、 B、 C、 D、6. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P = 40°,则∠ABC的度数为( )
A、 B、 C、 D、6. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P = 40°,则∠ABC的度数为( ) A、25° B、35° C、40° D、50°7. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与射线PA相切时,圆心O平移的距离为.cm.
A、25° B、35° C、40° D、50°7. 如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与射线PA相切时,圆心O平移的距离为.cm.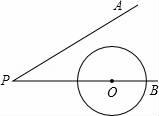 8. 如图,AB是⊙O的直径,CP切⊙O于点C,交AB的延长线于点P,若∠P=20°,则∠A=.
8. 如图,AB是⊙O的直径,CP切⊙O于点C,交AB的延长线于点P,若∠P=20°,则∠A=. 9. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=25°.求∠P的度数.
9. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=25°.求∠P的度数. 10. 如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .
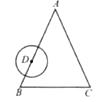
10. 如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .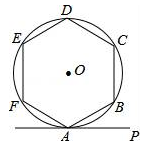 11. 如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
11. 如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.求证:AE平分∠CAB;

二、提高特训
-
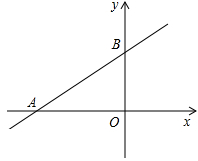
12. 已知⊙A与⊙B外切,⊙C与⊙A、⊙B都内切,且AB=5,AC=6,BC=7,那么⊙C的半径长是( )A、11 B、10 C、9 D、813. 已知⊙ 的半径为2,圆心在函数 的图象上运动,当⊙ 与坐标轴相切于点 时,则符合条件的点 的个数有( ).A、0个 B、1个 C、2个 D、4个14. 如图,⊙ 中,直径 与弦 相交于点 ,连接 ,过点 的切线与 的延长线交于点 ,若 ,则 的度数等于( )
 A、30° B、35° C、40° D、45°15. 已知 和 外切于 , 是 和 的外公切线, , 为切点,若 , ,则 到 的距离是( )
A、30° B、35° C、40° D、45°15. 已知 和 外切于 , 是 和 的外公切线, , 为切点,若 , ,则 到 的距离是( )
A、 B、 C、 D、