初中数学浙教版九年级下册2.1直线和圆的位置关系(2） 同步训练
试卷更新日期：2020-02-18 类型：同步测试
一、基础夯实
-
1. 行驶在水平路面上的汽车，若把路面看成直线，则此时转动的车轮与地面的位置关系是（ ）A、相交 B、相切 C、相离 D、不确定2. 已知⊙O的半径为5，直线EF经过⊙O上一点P（点E，F在点P的两旁），下列条件能判定直线EF与⊙O相切的是（ ）
A、OP=5 B、OE=OF C、O到直线EF的距离是4 D、OP⊥EF3. OA平分∠BOC，P是OA上任意一点（O除外），若以P为圆心的⊙P与OC相切，那么⊙P与OB的位置是（ ）A、相交 B、相切 C、相离 D、相交或相切4. 正方形ABCD中，点P是对角线AC上的任意一点（不包括端点），以P为圆心的圆与AB相切，则AD与⊙P的位置关系是（ ）A、相离 B、相切 C、相交 D、不确定5. 如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为 ．
6. 如图，点A，B，D在⊙O上，∠A＝25°，OD的延长线交直线BC于点C，若∠OCB＝40°，则直线BC与⊙O的位置关系为 ．
7. 阅读下面材料：在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：
尺规作图：过圆外一点作圆的切线．
已知：P为⊙O外一点．
求作：经过点P的⊙O的切线．
小敏的作法如下：
如图，
⑴连接OP ， 作线段OP的垂直平分线MN交OP于点C；
⑵以点C为圆心，CO的长为半径作圆，交⊙O于A ， B两点；
⑶作直线PA ， PB ． 所以直线PA ， PB就是所求作的切线．
老师认为小敏的作法正确．
请回答：连接OA ， OB后，可证∠OAP＝∠OBP＝90°，其依据是；由此可证明直线PA ， PB都是⊙O的切线，其依据是 ．
8. 如图，△ABC为等腰三角形，AB=AC，O是底边BC的中点，⊙O与腰AB相切于点D，求证：AC与⊙O相切．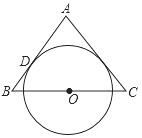
9. 已知：如图，在 中， ，以 为直径的 交 于点 ，过点 作 于点 .求证： 是 的切线.
10. 如图，已知AB是⊙O的直径，点C是AB延长线上的一点，点D在⊙O上且AD=CD，∠C=30°。
(1)、求证：CD是⊙O的切线，(2)、若⊙O的半径为5，求 的长。二、提高特训
-
11. 如图，AB是半圆O的直径，点C在半圆上(不与A，B重合)， 于点D，交BC于点F，下列条件中能判别 是切线的是（ ）
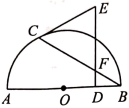A、 B、 C、 D、12. 如图，P为圆O外一点，OP交圆O于A点，且OA=2AP．甲、乙两人想作一条通过P点且与圆O相切的直线，其作法如下：（甲）以P为圆心，OP长为半径画弧，交圆O于B点，则直线PB即为所求；
（乙）作OP的中垂线，交圆O于B点，则直线PB即为所求．
对于甲、乙两人的作法，下列判断何者正确？（ ）
A、两人皆正确 B、两人皆错误 C、甲正确，乙错误 D、甲错误，乙正确13. 菱形的对角线相交于O，以O为圆心，以点O到菱形一边的距离为半径的⊙O与菱形其它三边的位置关系是（ ）A、相交 B、相离 C、相切 D、无法确定
