初中数学浙教版九年级下册2.1 直线和圆的位置关系(1) 同步训练
试卷更新日期:2020-02-18 类型:同步测试
一、基础夯实
-
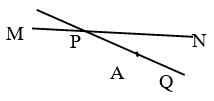
1. 圆的直径为13cm,如果圆心与直线的距离是d,则.( )A、当d=8cm,直线与圆相交. B、当d=4.5cm时,直线与圆相离. C、当d=6.5cm时,直线与圆相切. D、当d=13cm时,直线与圆相切.2. 已知⊙O的半径为5cm,如果圆心O到直线l的距离为5.5cm,那么直线l和⊙O的位置关系是( )A、相离 B、相切 C、相交 D、相交或相离3. 如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
 A、以PA为半径的圆 B、以PB为半径的圆 C、以PC为半径的圆 D、以PD为半径的圆4. 已知⊙O的半径为3,直线l上有一点P满足PO=3,则直线l与⊙O的位置关系是( )A、相切 B、相离 C、相离或相切 D、相切或相交5. 在平面直角坐标系 中,以点 为圆心,4为半径的圆( )A、与 轴相交,与 轴相切 B、与 轴相离,与 轴相交 C、与 轴相切,与 轴相交 D、与 轴相切,与 轴相离6. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )A、相离 B、相交 C、相切 D、以上三种情况均有可能7. 已知Rt△ABC中, , , ,如果以点 为圆心的圆与斜边 有唯一的公共点,那么 的半径 的取值范围为.8. 圆的半径为5cm , 如果圆心到直线的距离为3cm , 那么直线与圆有公共点的个数是 .9. 如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是 .10. 如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
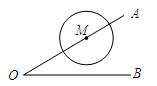
A、以PA为半径的圆 B、以PB为半径的圆 C、以PC为半径的圆 D、以PD为半径的圆4. 已知⊙O的半径为3,直线l上有一点P满足PO=3,则直线l与⊙O的位置关系是( )A、相切 B、相离 C、相离或相切 D、相切或相交5. 在平面直角坐标系 中,以点 为圆心,4为半径的圆( )A、与 轴相交,与 轴相切 B、与 轴相离,与 轴相交 C、与 轴相切,与 轴相交 D、与 轴相切,与 轴相离6. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )A、相离 B、相交 C、相切 D、以上三种情况均有可能7. 已知Rt△ABC中, , , ,如果以点 为圆心的圆与斜边 有唯一的公共点,那么 的半径 的取值范围为.8. 圆的半径为5cm , 如果圆心到直线的距离为3cm , 那么直线与圆有公共点的个数是 .9. 如果我们把太阳看作一个圆,把地平线看作一条直线,太阳在升起离开地平线后,太阳和地平线的位置关系是 .10. 如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.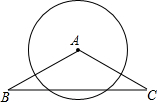 11. 如图,Rt△ABC中,∠C=90°,AC=3,AB=5,若以C为圆心,r为半径作圆,那么:
11. 如图,Rt△ABC中,∠C=90°,AC=3,AB=5,若以C为圆心,r为半径作圆,那么: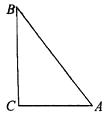 (1)、当直线AB与⊙C相切时,求r的取值范围;
(1)、当直线AB与⊙C相切时,求r的取值范围;
(2)、当直线AB与⊙C相离时,求r的取值范围;(3)、当直线AB与⊙C相交时,求r的取值范围.二、提高特训
-
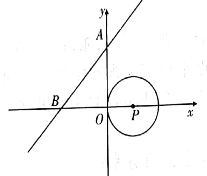
12. 已知⊙O的半径为10cm,弦MN∥E,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为( )cm.A、14或2 B、14 C、2 D、613. 如图,直线y=x+2与x轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P'的个数是( )
 A、2 B、3 C、4 D、614. 如图,在Rt△ABC中,BC=3cm,AC=4cm,动点P从点C出发,沿C→B→A→C运动,点P在运动过程中速度始终为1cm/s,以点C为圆心,线段CP长为半径作圆,设点P的运动时间为t(s),当⊙C与△ABC有3个交点时,此时t的值不可能是( )
A、2 B、3 C、4 D、614. 如图,在Rt△ABC中,BC=3cm,AC=4cm,动点P从点C出发,沿C→B→A→C运动,点P在运动过程中速度始终为1cm/s,以点C为圆心,线段CP长为半径作圆,设点P的运动时间为t(s),当⊙C与△ABC有3个交点时,此时t的值不可能是( ) A、2.4 B、3.6 C、6.6 D、9.615. Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )A、当r=2时,直线AB与⊙C相交 B、当r=3时,直线AB与⊙C相离 C、当r=2.4时,直线AB与⊙C相切 D、当r=4时,直线AB与⊙C相切16. 如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是.
A、2.4 B、3.6 C、6.6 D、9.615. Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )A、当r=2时,直线AB与⊙C相交 B、当r=3时,直线AB与⊙C相离 C、当r=2.4时,直线AB与⊙C相切 D、当r=4时,直线AB与⊙C相切16. 如图,已知∠BOA=30°,M为OA边上一点,以M为圆心、2cm为半径作⊙M.点M在射线OA上运动,当OM=5cm时,⊙M与直线OB的位置关系是.