湖北省孝感市（应城市，安陆市，云梦县)2019届九年级数学4月联考试卷

试卷更新日期：2020-02-17 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{5}$ 的倒数是（）

A、 $- 5$ B、5 C、 $\frac{1}{5}$ D、25

查看试题解析
2. 如图， $A B / / C D$ ， $∠ 1 = 50 °$ ， $∠ 2 = 45 °$ ，则 $∠ C A D$ 的大小是（）

A、 $75 °$ B、 $80 °$ C、 $85 °$ D、 $90 °$

查看试题解析
3. 下列计算正确的是（）

A、 $3 a - 4 a = a$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $a^{8} \div a^{2} = a^{4}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
4. 我市气象部门测得某周内七天的日温差数据如下：4，6，6，5，7，6，8（单位：℃），这组数据的平均数和众数分别是（　　）

A、7，6 B、6，5 C、5，6 D、6，6

查看试题解析
5. 如图，在 $Δ A B C$ 中， $A B = 8$ ， $A C = 6$ ， $O$ 为 $Δ A B C$ 角平分线的交点，若 $Δ A B O$ 的面积为20，则 $Δ A C O$ 的面积为是（）

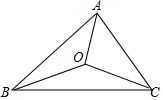A、12 B、15 C、16 D、18

查看试题解析
6. 若关于 $x$ 的一元一次不等式组 ${\begin{matrix} 2 x - 1 < 3 (x - 2) \\ x > m \end{matrix}$ 的解集是 $x > 5$ ，则实数 $m$ 的取值范围是（）

A、 $m \leq 5$ B、 $m < 5$ C、 $m \geq 5$ D、 $m > 5$

查看试题解析
7. 如图，在Rt△ABC中，∠ACB=90°，斜边AB的垂直平分线交AB于点D，交BC于点E，已知AB=5，AC=3，则△ACE的周长为（）

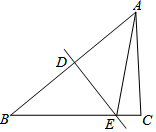A、5 B、6 C、7 D、8

查看试题解析
8. 如图是由棱长为1的正方体搭成的某几何体三视图，则图中棱长为1的正方体的个数是（）

A、5 B、6 C、7 D、8

查看试题解析
9. 如图，矩形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，连接BD交AF于H，AD=10 $\sqrt{2}$ ，且tan∠EFC= $\frac{\sqrt{2}}{4}$ ，那么AH的长为（）

A、 $\frac{10 \sqrt{6}}{3}$ B、 $5 \sqrt{2}$ C、10 D、5

查看试题解析
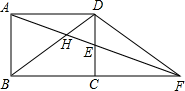10. 如图，二次函数y=ax²+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y₁），若点D（x₂ ， y₂）是抛物线上任意一点，有下列结论：①二次函数y=ax²+bx+c的最小值为﹣4a；②若﹣1≤x₂≤4，则0≤y₂≤5a；③若y₂＞y₁ ，则x₂＞4；④一元二次方程cx²+bx+a=0的两个根为﹣1和 $\frac{1}{3}$ 其中正确结论的个数是（）

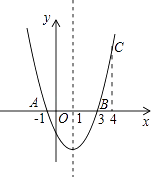A、1 B、2 C、3 D、4

查看试题解析

二、填空题

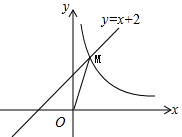
11. 2019年春运3月1日顺利结束.交通运输部2日发布的数据显示，春运40天，全国旅客发送量达29.8亿人次.将数据“29.8亿”用科学记数法表示为.

查看试题解析
12. 点 $A (m - 1, - 2)$ 与点 $B (3, n + 1)$ 关于原点对称，则 $m + n =$ .

查看试题解析
13. 分解因式： $(a + 2) (a - 2) + 3 a =$ .

查看试题解析
14. 如图，一次函数 $y = x + 2$ 与反比例函数 $y = \frac{k}{x}$ 的图像在第一象限交于点 $M$ ，若 $O M = \sqrt{10}$ ，则 $k$ 的值是.

查看试题解析
15. 如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP＋BP的值最小时，BP与HG的夹角(锐角)度数为．

查看试题解析

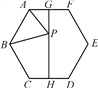
三、解答题

16. 计算： $| - 4 | + {(\frac{1}{2})}^{- 1} + \sqrt{8} - 4 \sin 45 °$

查看试题解析
17. 如图，四边形 $A B C D$ 是平行四边形， $E$ 、 $F$ 在对角线 $A C$ 上，且 $A E = C F$ ，连接 $B E$ ， $D E$ ， $B F$ ， $D F$ .求证 $∠ 1 = ∠ 2$ .

查看试题解析
18. 如图，在矩形 $A B C D$ 中，小聪同学利用直尺和圆规完成了如下操作：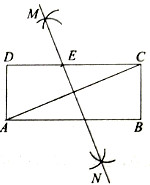

①分别以点 $A$ 和 $C$ 为圆心，以大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于点 $M$ 和 $N$ ；

②作直线 $M N$ ，交 $C D$ 于点 $E$ .

请你观察图形解答下列问题：

(1)、 $M N$ 与 $A C$ 的位置关系：
直线 $M N$ 是线段 $A C$ 的线；

(2)、若 $D E = 3$ ， $C E = 4$ ，求矩形的对角线 $A C$ 的长.

查看试题解析
19. 某中学就“戏曲进校园”活动的喜爱情况进行了随机调查，对收集的信息进行了统计，绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题：（图中 $A$ 表示“很喜欢”， $B$ 表示“喜欢”， $C$ 表示“一般”， $D$ 表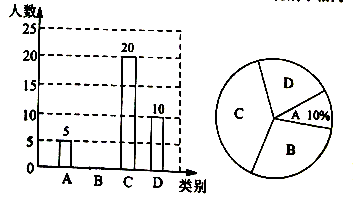示“不喜欢”）

(1)、被调查的总人数是，扇形统计图中 $C$ 部分所对应的扇形圆心角的度数为；

(2)、补全条形统计图；

(3)、在抽取的 $A$ 类5人中，刚好有甲、乙、丙3个女生和丁、戊2个男生，从中随机抽取两个同学担任两角色，用画树状图或列表法求出抽到的两个学生性别不相同的概率.

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + (m - 5) x + 1 - m = 0$ ，其中 $m$ 为常数.

(1)、求证：无论 $m$ 为何值，方程总有两个不相等实数根；

(2)、若抛物线 $y = x^{2} + (m - 5) x + 1 - m$ 与 $x$ 轴交于 $A (x_{1}, 0)$ 、 $B (x_{2}, 0)$ 两点，且 $| x_{1} - x_{2} | = 4$ ，求 $m$ 的值；

查看试题解析
21. 五一期间，某商场计划购进甲、乙两种商品，已知购进甲商品1件和乙商品3件共需240元；购进甲商品2件和乙商品1件共需130元.

(1)、求甲、乙两种商品每件的进价分别是多少元？

(2)、商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润.

查看试题解析
22. 如图， $A$ ， $B$ ， $C$ 三点在 $⊙ O$ 上，直径 $B D$ 平分 $∠ A B C$ ，过点 $D$ 作 $D E / / A B$ 交弦 $B C$ 于点 $E$ ，在 $B C$ 的延长线上取一点 $F$ ，使得 $E F = E D$ .

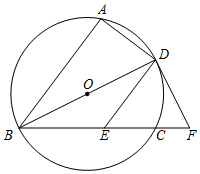(1)、求证： $D F$ 是 $⊙ O$ 的切线；

(2)、连接AF交DE于点M，若AD=4，DE=5，求DM的长．

查看试题解析
23. 如图，抛物线y=x²+bx+c与x轴交于A（-1，0）、B（3，0）两点．

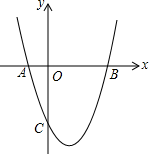(1)、求该抛物线的解析式；

(2)、设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S_△_PAB=10，并求出此时P点的坐标；

(3)、设（1）中的抛物线交y轴交于C点，在该抛物线的对称轴上是否存在点Q，使△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．

查看试题解析