河南省周口市沈丘县2019届九年级数学中考一模试卷

试卷更新日期：2020-02-17 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\sqrt{2}$ 的绝对值是（）

A、 $\sqrt{2}$ B、- $\sqrt{2}$ C、 $\pm \sqrt{2}$ D、 $\frac{1}{\sqrt{2}}$

查看试题解析
2. 2015年诺贝尔医学奖得主中国科学家屠呦呦，发现了一种病毒的长度约为0.00000456毫米，则数据0.00000456用科学记数法表示为（）

A、0.456×10^﹣⁵ B、4.56×10^﹣⁶ C、4.56×10^﹣⁷ D、45.6×10^﹣⁸

查看试题解析
3. 如图是用小正方体搭成的几何体的主视图和俯视图，俯视图上的数字表示小正方体的个数，则搭这个几何体最多需要的小正方体的个数为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况，下列说法中正确的是（）

A、中位数是52.5 B、众数是8 C、众数是52 D、中位数是53

查看试题解析
5. 有两个一元二次方程M：ax²+bx+c＝0，N：cx²+bx+a＝0，其中a+c＝0，下列四个结论中，错误的是（）

A、如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 B、b＝0时，方程M和方程N有一个相同的根，那么这个根必是x＝1 C、如果5是方程M的一个根，那么 $\frac{1}{5}$ 是方程N的一个根 D、ac≠0

查看试题解析
6. 如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，下列条件中，不能使四边形DBCE成为菱形的是（）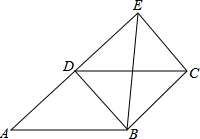

A、AB＝BE B、BE⊥DC C、∠ABE＝90° D、BE平分∠DBC

查看试题解析
7. 从﹣2，﹣1，2这三个数中任取两个不同的数相乘，积为正数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
8. 如图，在平面直角坐标系中，正方形OABC的顶点O、B的坐标分别是（0，0），（2，0），则顶点C的坐标是（）

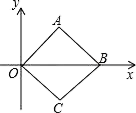A、（1，1） B、（﹣1，﹣1） C、（1，﹣1） D、（﹣1，1）

查看试题解析
9. 如图，在矩形ABCD中AB＝ $\sqrt{2}$ ，BC＝1，将矩形ABCD绕顶点B旋转得到矩形A'BC'D，点A恰好落在矩形ABCD的边CD上，则AD扫过的部分（即阴影部分）面积为（）

A、 $\frac{π}{8}$ B、 $2 \sqrt{2} - \frac{π}{2}$ C、 $\sqrt{2} - \frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析

二、填空题

10. 计算： ${(- 2)}^{3} + \sqrt{9} =$ ．

查看试题解析
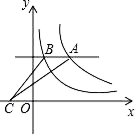
11. 若不等式组 ${\begin{array}{l} x - a > 1 \\ b x + 3 \geq 0 \end{array}$ 的解集是﹣1＜x≤1，则a＝， b＝．

查看试题解析
12. 如图，平行于x轴的直线与函数 $y = \frac{k_{1}}{x}$ （k₁＞0，x＞0）和 $y = \frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象分别相交于A，B两点．点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k₁﹣k₂的值为．

查看试题解析
13. 如图1，点 $E$ ， $F$ ， $G$ 分别是等边三角形 $A B C$ 三边 $A B$ ， $B C$ ， $C A$ 的动点，且始终保持 $A E = B F = C G$ ，设 $△ E F G$ 的面积为 $y$ ， $A E$ 的长为 $x$ ， $y$ 关于 $x$ 的函数图象大致为图2所示，则等边三角形 $A B C$ 的边长为．

查看试题解析
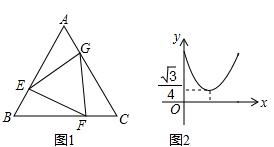14. 在△ABC中，∠BAC=90°，AB=AC，点D在BC边上，把△ABD沿AD折叠后，使得点B落在点E处，连接CE，若∠DBE=20°，则∠ADC=.

查看试题解析

三、解答题

15. 先化简，再求值：（x+y）（x﹣y）﹣（x﹣y）²﹣y（x﹣2y），其中x＝2019，y＝ $\frac{1}{2019}$ ．

查看试题解析

16. 诗词是我国古代文化中的瑰宝，某市教育主管部门为了解本市初中生对诗词的学习情况，举办了一次“中华诗词”背诵大赛，随机抽取了部分同学的成绩(x为整数，总分100分)，绘制了如下尚不完整的统计图表．

组别	成绩分组(单位：分)	频数
A	50≤x＜60	40
B	60≤x＜70	a
C	70≤x＜80	90
D	80≤x＜90	b
E	90≤x＜100	100
合计		c

根据以上信息解答下列问题：

(1)、统计表中a＝， b＝， c＝；

(2)、扇形统计图中，m的值为， “E”所对应的圆心角的度数是(度)；

(3)、若参加本次大赛的同学共有4000人，请你估计成绩在80分及以上的学生大约有多少人？

查看试题解析

17. 如图，钝角△ABC中，AB=AC，BC=2 $\sqrt{3}$ ，O是边AB上一点，以O为圆心，OB为半径作⊙O，交边AB于点D，交边BC于点E，过E作⊙O的切线交边AC于点F．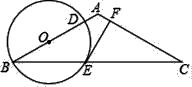

(1)、求证：EF⊥AC．

(2)、连结DF，若∠ABC=30°，且DF∥BC，求⊙O的半径长．

查看试题解析
18. 如图为某区域部分交通线路图，其中直线 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线 $l$ 与直线 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 都垂直，垂足分别点 $A$ 、点 $B$ 和点 $C$ ，（高速路右侧边缘）， $l_{2}$ 上的点 $M$ 位于点 $A$ 的北偏东 $30 °$ 方向上，且 $B M = 3 \sqrt{3}$ 千米， $l_{3}$ 上的点 $N$ 位于点 $M$ 的北偏东 $α$ 方向上，且 $\cos α = \frac{\sqrt{13}}{13}$ ， $M N = 2 \sqrt{13}$ 千米．点 $A$ 和点 $N$ 是城际线 $L$ 上的两个相邻的站点．

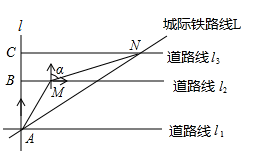(1)、求 $l_{2}$ 和 $l_{3}$ 之间的距离；

(2)、若城际火车平均时速为 $150$ 千米/小吋，求市民小强乘坐城际火车从站点 $A$ 到站点 $N$ 需要多少小时？（结果用分数表示）

查看试题解析
19. 如图，一次函数y＝k₁x+b与反比例函数 $y = \frac{k_{2}}{x}$ 的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S_△_ABC＝5．

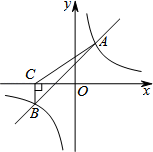(1)、求一次函数与反比例函数的解析式．

(2)、根据所给条件，请直接写出不等式k₁x+b＞ $\frac{k_{2}}{x}$ 的解集；

(3)、若P（p，y₁），Q（﹣2，y₂）是函数y＝ $\frac{k_{2}}{x}$ 图象上的两点，且y₁≥y₂ ，求实数p的取值范围．

查看试题解析

20. 小明购买A，B两种商品，每次购买同一种商品的单价相同，具体信息如下表：

次数	购买数量（件 $)$		购买总费用（元 $)$
次数	A	B	购买总费用（元 $)$
第一次	2	1	55
第二次	1	3	65

根据以上信息解答下列问题：

(1)、求A，B两种商品的单价；

(2)、若第三次购买这两种商品共12件，且A种商品的数量不少于B种商品数量的2倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析

21. 观察猜想

(1)、如图①，在 $Rt △ A B C$ 中， $∠ B A C = 90^{°}$ ， $A B = A C = 3$ ，点 $D$ 与点 $A$ 重合，点 $E$ 在边 $B C$ 上，连接 $D E$ ，将线段 $D E$ 绕点 $D$ 顺时针旋转90°得到线段 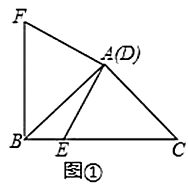$D F$ ，连接 $B F$ ， $B E$ 与 $B F$ 的位置关系是， $B E + B F =$ ；

(2)、在（1）中，如果将点 $D$ 沿射线 $A B$ 方向移动，使 $A D = 1$ ，其余条件不变，如图②判断 $B E$ 与 $B F$ 的位置关系，并求 $B E + B F$ 的值，请写出你的理由或计算过程；

(3)、如图③，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = α$ ，点 $D$ 在 $B A$ 的延长线上， $B D = n$ ，连接 $D E$ ，将线段 $D E$ 绕点 $D$ 顺时针旋转，旋转角 $∠ E D F = α$ ，连接 $B F$ ，则 $B E + B F$ 的值是多少？请用含有 $n$ ， $α$ 的式子直接写出结论.

查看试题解析
22. 如图，已知二次函数 $y = - x^{2} + b x + c (c > 0)$ 的图象与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ，且 $O B = O C = 3$ ，顶点为 $M$ ．

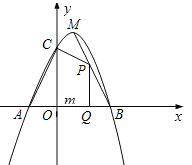(1)、求二次函数的解析式；

(2)、点 $P$ 为线段 $B M$ 上的一个动点，过点 $P$ 作 $x$ 轴的垂线 $P Q$ ，垂足为 $Q$ ，若 $O Q = m$ ，四边形 $A C P Q$ 的面积为 $S$ ，求 $S$ 关于 $m$ 的函数解析式，并写出 $m$ 的取值范围；

(3)、探索：线段 $B M$ 上是否存在点 $N$ ，使 $△ N M C$ 为等腰三角形？如果存在，求出点 $N$ 的坐标；如果不存在，请说呀理由．

查看试题解析