浙江省2020届九年级上学期创新体验营测试数学试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、选择题（本大题7×5分=35分，只有一个选项正确）

1. 以下说法正确的是（）

A、存在锐角 $θ$ ，使得sin² $θ$ +cos² $θ$ >1 B、已知∠A为Rt△ABC的一个内角，且∠A<45°，则sinA<cosA C、在Rt△ABC中，∠C=90°，∠A，∠B为Rt△ABC的两个内角，则sinA不一定等于cosB D、存在锐角 $θ$ ，使得sin $θ$ ≥tan $θ$

查看试题解析
2. 小王在word文档中设计好一张A4规格的表格，根据要求，这种规格的表格需要设计1000张，小王欲使用“复制——粘贴”（用鼠标选中表格，右键点击“复制”，然后在本word文档中“粘贴”）的办法满足要求。请问：小王需要使用“复制——粘贴“的次数至少为（）

A、9次 B、10次 C、11次 D、12次

查看试题解析
3. 已知a是实数。则以下式子一定正确的是（）。

A、 $\sqrt{a^{2}} = a$ B、 $a^{3} = a^{2}$ C、 ${(\sqrt{a})}^{2} = a$ D、关于 $a$ 的方程 $\sqrt{a^{2} + 1} = \sqrt{2} a$ 的实数解是 $\pm 1$

查看试题解析
4. 已知 $\frac{(\sqrt{2 + 1}) b - c}{(3 + 2 \sqrt{2}) a} = 1 (a ， b ， c \in R)$ ，则有（）

A、 $b^{2} > 4 a c$ B、 $b^{2} \geq 4 a c$ C、 $b^{2} < 4 a c$ D、 $b^{2} \leq 4 a c$

查看试题解析
5. 布鲁斯先生、他的妹妹、他的儿子，还有他的女儿都是网球选手．这四人中有以下情况：
①最佳选手的孪生同胞与最差选手性别不同：②最佳选手与最差选手年龄相同．则这四人中最佳选手是（ )

A、布普斯先生 B、布鲁斯先生的妹妹 C、布鲁斯先生的儿子 D、布鲁斯先生的女儿

查看试题解析
6. 从1、2、3、……、2018、2019中挑选一些数，其中没有两数之和可以被其差整除，选出的这些数最多有（）

A、672个 B、673个 C、674个 D、以上都不对

查看试题解析
7. 若四边形A鱿O的对角线AC，BD相交于O，△AOB，△BOC，△COD，△DOA的周长相等，且△AOB，△BOC，△COD的内切圆半径分别为3，4，6，则△DOA的内切圆半径是（ )

A、 $\frac{9}{2}$ B、 $\frac{3}{2}$ C、 $\frac{7}{2}$ D、以上答案均不正确

查看试题解析

二、填空题（本大题7×5分=35分，把答案填在答题卷横线上）

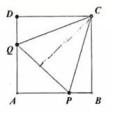
8. 已知a，b，c为三个非零实数， $x^{2} - 1$ 为多项式 $x^{3} + a x^{2} + b x + c$ 的因式．则 $\frac{a b + 3 a}{c}$ 的值为.

查看试题解析
9. 如图，正方形ABCD的边长为1，P，Q分别为AB，DA上的点，当△APQ的周长为2时，则 $∠ P C Q$ =·

查看试题解析
10. 若方程 $x^{2} - 3 x + 1 = 0$ 的根也是方程 $x^{4} + a x^{2} + b x + c = 0$ 的根，则 $a + b + 2 c =$ .

查看试题解析
11. 某人掷两枚质地均匀的般子（般子的六个面分别为l点，2点，3点，4点，5点，6点），则该人掷一次出现两枚般子点数和为6的概率是.

查看试题解析
12. 我们知道平面内到两个定点距离之比为常数（常数大于零且不为1）的点轨迹是一个圆，那么在平面直角坐标系内到原点（0，0）和点（3，0）距离之比为2的圆的圆心坐标是.

查看试题解析
13. 对于正整数n定义阶乘 $n! = 1 \times 2 \times 3 \times \dots \times （ n - 1 ） \times n$ ，则 $1 \times 1! + 2 \times 2! + 3 \times 3! + \dots + 100 \times 100! =$ （用阶乘表示）

查看试题解析
14. 已知正实数a、b、c满足 $a^{2} + b^{2} + c^{2} - a c - b c = 1$ ．则c的最大值是.

查看试题解析

三、解答题（本大题5x16分＝80分，解答应写出必要的文字说明、证明过程及演算步骤）

15. 在多项式中有一类比较有趣的因式分解，如我们已经学过的
$1 - x^{2} = (1 - x) \cdot (1 + x)$

$1 - x^{3} = (1 - x) \cdot (1 + x + x^{2})$

(1)、证明： $1 - x^{4} = (1 - x) \cdot (1 + x + x^{2} + x^{3})$ ；

(2)、据此猜想，对任意正整数 $n \geq 2 ， 1 - x^{n} =$ （不必证明）；

(3)、利用（2），求 $\frac{1}{2} + {(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{3} + ... + {(\frac{1}{2})}^{2019}$ 的值

查看试题解析
16. 设a，b为实数，关于x的方程 $\frac{x}{x - 1} + \frac{x - 1}{x} = \frac{a + b x}{x^{2} - x}$ 无实数根，求代数式 $8 a + 4 b + | 8 a + 4 b - 5 |$ 的值.

查看试题解析
17. 已知如图．在四边形ABCD中． $∠ B A D = ∠ B C D$ ，点E、F、G、H分别是各边中点．

(1)、求证： $∠ E G F = ∠ E H F$ ；

(2)、求证： $∠ D H G = ∠ D B A - ∠ D B C$

查看试题解析
18. 已知对任意正整数n，定义 $f (n) = \frac{1}{1 + 2 + 3 + ... + n}$

(1)、求 $f (1) + f (2) + f (3) ＋ \dots ＋ f (2018) + f (2019)$ 的值；

(2)、求证： $\frac{3}{2} < \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} ＋ \dots ＋ \frac{1}{2018^{2}} + \frac{1}{2019^{2}} < 2$

查看试题解析
19. 如图，M为锐角△ABC边BC的中点，圆O过点A且与直线BC切于点C，直线AM与圆O的第二个交点为D，直线BD与圆O的第二个交点为E．求证： $∠ E A C = ∠ B A C$

查看试题解析

浙江省2020届九年级上学期创新体验营测试数学试卷

一、 选择题（本大题7×5分=35分，只有一个选项正确）

二、填空题（本大题7×5分=35分，把答案填在答题卷横线上）

三、解答题（本大题5x16分＝80分，解答应写出必要的文字说明、证明过程及演算步骤）

一、选择题（本大题7×5分=35分，只有一个选项正确）