河南省信阳市淮滨县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 下面有四个图案,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是 ( )A、a3+a2=a5 B、a3 •a2 =a5 C、(2a2 )3=6a6 D、a6÷(+a2 )=a33. 画△ABC的边AC上的高BE,以下画图正确的是( )A、
2. 下列计算正确的是 ( )A、a3+a2=a5 B、a3 •a2 =a5 C、(2a2 )3=6a6 D、a6÷(+a2 )=a33. 画△ABC的边AC上的高BE,以下画图正确的是( )A、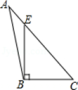 B、
B、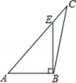 C、
C、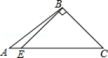 D、
D、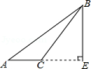 4. 若分式 的值为零,则x的值为( )A、-2 B、±2 C、2 D、15. 下列从左到右的运算是因式分解的是 ( )A、4a -4a+1=4a(a-1)+1 B、(x-y)(x+y)=x -y C、x +y =(x+y) -2xy D、(xy) -1=(xy+1)(xy-1)6. 叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米.其中,0.00005用科学记数法表示为( )A、0.5×10﹣4 B、5×10﹣4 C、5×10﹣5 D、50×10﹣37. 如图,已知AO=CO,那么添加下列一个条件后,仍无法判定△ABO ≌△CDO 的是( )
4. 若分式 的值为零,则x的值为( )A、-2 B、±2 C、2 D、15. 下列从左到右的运算是因式分解的是 ( )A、4a -4a+1=4a(a-1)+1 B、(x-y)(x+y)=x -y C、x +y =(x+y) -2xy D、(xy) -1=(xy+1)(xy-1)6. 叶绿体是植物进行光合作用的场所,叶绿体DNA最早发现于衣藻叶绿体,长约0.00005米.其中,0.00005用科学记数法表示为( )A、0.5×10﹣4 B、5×10﹣4 C、5×10﹣5 D、50×10﹣37. 如图,已知AO=CO,那么添加下列一个条件后,仍无法判定△ABO ≌△CDO 的是( ) A、∠A=∠C B、BO=DO C、AB=CD D、∠B=∠D8. 如图,将一个正方形剪去一个角后,∠1+∠2 等于( )
A、∠A=∠C B、BO=DO C、AB=CD D、∠B=∠D8. 如图,将一个正方形剪去一个角后,∠1+∠2 等于( )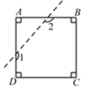 A、120° B、170° C、220° D、270°9. 到三角形三个顶点的距离都相等的点是这个三角形的( )A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点10. 如图,已知△ABC中,AB=7,AC=5,BC=3,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( )
A、120° B、170° C、220° D、270°9. 到三角形三个顶点的距离都相等的点是这个三角形的( )A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点10. 如图,已知△ABC中,AB=7,AC=5,BC=3,在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3的等腰三角形,则这样的直线最多可画( ) A、2条 B、3条 C、4条 D、5条
A、2条 B、3条 C、4条 D、5条二、填空题
-
11. 点M 关于y轴的对称点的坐标为 .12. 分解因式:3x2-6x+3= .13. 若三角形的两边长是5 和2 ,且第三边的长度是偶数,则第三边长可能是 .14. 如图,在△ABC中,BF⊥AC 于点F,AD⊥BC 于点D ,BF 与AD 相交于点E.若AD=BD,BC=8cm,DC=3cm.则 AE= cm .
 15. 化简:a+1+a(a+1)+a(a+1)2+…+a(a+1)99= .
15. 化简:a+1+a(a+1)+a(a+1)2+…+a(a+1)99= .三、解答题
-
16. 已知 ,求代数式 的值。17. 先化简: ,再从 的范围内选取一个合适的整数作为 的值代入求值.18. 如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
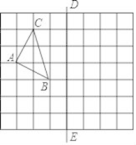
①画出格点△ABC关于直线DE的对称的△A1B1C1;
②在DE上画出点P,使PA+PC最小;
③在DE上画出点Q,使QA﹣QB最大.
19. 如图,已知D,E在三角形ABC的边BC上,且AB=AC,AD=AE。求证:BD=CE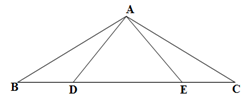 20. 列方程解应用题:
20. 列方程解应用题:中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
21. 如图,AB=CD,DE⊥AC,BF⊥AC,点E,F是垂足,AE=CF,求证: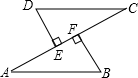 (1)、△ABF≌△CDE;(2)、AB∥CD.22. 分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如,分式 是真分式,如果分子的次数不低于分母的次数,称这样的分式为假分式,例如,分式 是假分式,一个假分式可以化为一个整式与一个真分式的和,例如, .(1)、将假分式 化为一个整式与一个真分式的和;(2)、若分式 的值为整数,求 的整数.23. 在△ABC中,AB=AC,点D 在底边BC 上,AE=AD,连接 DE.
(1)、△ABF≌△CDE;(2)、AB∥CD.22. 分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如,分式 是真分式,如果分子的次数不低于分母的次数,称这样的分式为假分式,例如,分式 是假分式,一个假分式可以化为一个整式与一个真分式的和,例如, .(1)、将假分式 化为一个整式与一个真分式的和;(2)、若分式 的值为整数,求 的整数.23. 在△ABC中,AB=AC,点D 在底边BC 上,AE=AD,连接 DE.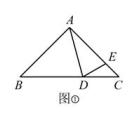
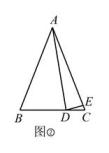 (1)、如图①,已知∠BAC=90°,∠BAD=60°,求 ∠CDE 的度数;(2)、如图①,已知∠BAC=90°,当点D 在线段BC(点B,C 除外)上运动时,试探究∠BAD与∠CDE的数量关系;(3)、如图②,若 ∠BAC≠90°,试探究∠BAD与 ∠CDE 的数量关系.
(1)、如图①,已知∠BAC=90°,∠BAD=60°,求 ∠CDE 的度数;(2)、如图①,已知∠BAC=90°,当点D 在线段BC(点B,C 除外)上运动时,试探究∠BAD与∠CDE的数量关系;(3)、如图②,若 ∠BAC≠90°,试探究∠BAD与 ∠CDE 的数量关系.