辽宁省抚顺市新宾县2019年数学中考二模试卷
试卷更新日期:2020-02-17 类型:中考模拟
一、单选题
-
1. 把图形
 绕 点顺时针旋转 度后,得到的图形是( ) A、
绕 点顺时针旋转 度后,得到的图形是( ) A、 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标为( )A、(-1,2) B、(1,2) C、(1,-2) D、(2,1)3. 方程 的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根4. 半径为5的 ,圆心在直角坐标系的原点 ,则点 与 的位置关系是A、在 上 B、在 内 C、在 外 D、不能确定5. 已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆周角的度数为( )A、45° B、90° C、90° 或27° D、45°或135°6. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、
2. 抛物线 的顶点坐标为( )A、(-1,2) B、(1,2) C、(1,-2) D、(2,1)3. 方程 的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个实数根4. 半径为5的 ,圆心在直角坐标系的原点 ,则点 与 的位置关系是A、在 上 B、在 内 C、在 外 D、不能确定5. 已知弦AB把圆周分成1:3的两部分,则弦AB所对的圆周角的度数为( )A、45° B、90° C、90° 或27° D、45°或135°6. 在同一平面直角坐标系中,函数 与 的图象可能是( )A、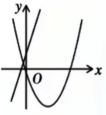
B、
B、
C、
C、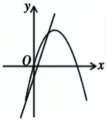
D、
D、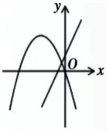
7. 为解决民生问题,国家对某药品价格分两次降价,该药品的原价是48元,降价后的价格是30元,若平均每次降价的百分率均为 ,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( ).
7. 为解决民生问题,国家对某药品价格分两次降价,该药品的原价是48元,降价后的价格是30元,若平均每次降价的百分率均为 ,可列方程为( )A、 B、 C、 D、8. 如图,在△ABC中,AB=3,AC=2,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( ).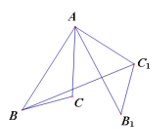 A、
A、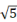 B、
B、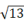 C、4
D、6
9. 如图,D是等腰△ABC外接圆弧AC上的点,AB=AC且∠CAB=56°,则∠ADC的度数为( )
C、4
D、6
9. 如图,D是等腰△ABC外接圆弧AC上的点,AB=AC且∠CAB=56°,则∠ADC的度数为( )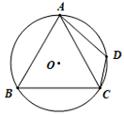 A、116° B、118° C、122° D、126°10. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△AB1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去……,若点A( ,0),B(0,2).则点B2019的坐标是( )
A、116° B、118° C、122° D、126°10. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△AB1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去……,若点A( ,0),B(0,2).则点B2019的坐标是( )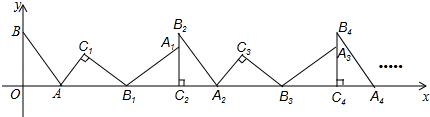 A、(6052,0) B、(6054,2) C、(6058,0) D、(6060,2)
A、(6052,0) B、(6054,2) C、(6058,0) D、(6060,2)二、填空题
-
11. 若点 与 关于原点对称,则 的值是.12. 关于x的一元二次方程kx2﹣4x+3=0有实数根,则k应满足的条件是.13. 如果二次函数 的图像经过原点,那么 的值是.14. 如果点 、 是二次函数 的图像上两点,那么 .(填“>”、“=”或“<”)15. 如图,是4×4正方形网格,其中已有三个小方格涂成黑色,在剩下的13个白色小方格中随意选一个涂成黑色,使得黑色小方格组成的图形为轴对称图形的涂法有种
 16. 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2,EM=4,则⊙O的半径为 .
16. 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2,EM=4,则⊙O的半径为 .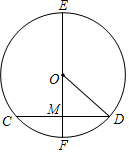 17. 把一元二次方程x2+6x-1=0通过配方化成(x+m)2= n的形式为 .18. 二次函数y=x2的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…∁n在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAn∁n都是正方形,则正方形An﹣1BnAn∁n的周长为 .
17. 把一元二次方程x2+6x-1=0通过配方化成(x+m)2= n的形式为 .18. 二次函数y=x2的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…∁n在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAn∁n都是正方形,则正方形An﹣1BnAn∁n的周长为 .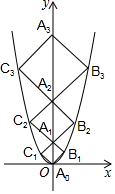
三、解答题
-
19.(1)、计算:(2)、解方程:9x2﹣6x+1=020. 如图,已知平面直角坐标系中,△ABC的顶点坐标分别A(1,3),B(2,1),C(4,2).

①将△ABC以原点O为旋转中心旋转180°得到△A1B1C1 , 画出△A1B1C1;
②平移△ABC,使点A的对应点A2坐标为(5,﹣5),画出平移后的△A2B2C2;
③若将△A1B1C1绕某一点旋转可得到△A2B2C2 , 请直接写出这个点的坐标.
21. 如图,AB是⊙O直径,CD为⊙O的切线,C为切点,过A作CD的垂线,垂足为D.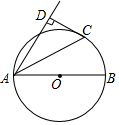 (1)、求证:AC平分∠BAD;(2)、若⊙O半径为5,CD=4,求AD的长.22. 如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).
(1)、求证:AC平分∠BAD;(2)、若⊙O半径为5,CD=4,求AD的长.22. 如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).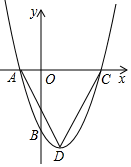 (1)、求抛物线的解析式及顶点D的坐标.(2)、求△ACD的面积.23. 某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量 (件)与销售单价 (元)之间的关系可近似地看作一次函数 .物价部门规定该品牌的护眼灯售价不能超过36元.(1)、如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?(2)、设该商店每月获得利润为 (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?24. 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)、求抛物线的解析式及顶点D的坐标.(2)、求△ACD的面积.23. 某灯饰商店销售一种进价为每件20元的护眼灯.销售过程中发现,每月销售量 (件)与销售单价 (元)之间的关系可近似地看作一次函数 .物价部门规定该品牌的护眼灯售价不能超过36元.(1)、如果该商店想要每月获得2000元的利润,那么销售单价应定为多少元?(2)、设该商店每月获得利润为 (元),当销售单价定为多少元时,每月可获得最大利润?最大利润为多少元?24. 如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.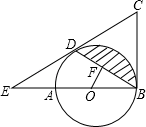 (1)、求证:CD为⊙O的切线;(2)、若OF⊥BD于点F,且OF=2,BD=4 ,求图中阴影部分的面积.25. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 .
(1)、求证:CD为⊙O的切线;(2)、若OF⊥BD于点F,且OF=2,BD=4 ,求图中阴影部分的面积.25. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 . (1)、请求出旋转角的度数;(2)、请判断 与 的位置关系,并说明理由;(3)、若 , ,试求出四边形 的对角线 的长.26. 如图,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)、请求出旋转角的度数;(2)、请判断 与 的位置关系,并说明理由;(3)、若 , ,试求出四边形 的对角线 的长.26. 如图,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
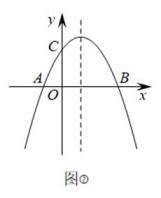 (1)、求该抛物线的解析式;(2)、如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.