重庆市合川区2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

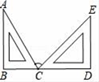
1. 在数0，2，－3，－1.2中，属于负整数的是( )

A、0　　 B、2　　 C、－3　 D、－1.2

查看试题解析
2. 下列方程中，是一元一次方程的是（　　）

A、x+2y＝9 B、x²﹣3x＝6 C、 $\frac{1}{x - 1}$ ＝2 D、 $\frac{x - 1}{2}$ ﹣ $\frac{x + 1}{3}$ ＝1

查看试题解析
3. 用一副三角板拼成的图形如图所示，其中B，C，D三点在同一条直线上.则图中∠ACE的大小为（　　）

A、45° B、60° C、75° D、105°

查看试题解析
4. 单项式 $\frac{5 x^{2} y}{3}$ 的系数与次数分别是（）

A、 $\frac{5}{3}$ 和3 B、﹣5和3 C、 $\frac{5}{3}$ 和2 D、﹣5和2

查看试题解析
5. 已知a=﹣ $\frac{1}{2}$ ，b=﹣1，c=0.1，则a、b、c的大小关系是（　　）

A、b＜a＜c B、a＜b＜c C、c＜a＜b D、c＜b＜a

查看试题解析
6. 下列四个图形中是正方体的平面展开图的是（　　）

A、 B、 C、 D、

查看试题解析
7. 下列运算正确的是（　　）

A、﹣1²⁰¹⁸＝1 B、3³＝9 C、﹣3﹣2＝﹣1 D、（﹣2）×（﹣3）＝6

查看试题解析
8. 已知x²﹣xy＝30，xy﹣y²＝14，则x²﹣2xy+y²等于（　　）

A、49 B、16 C、44 D、9

查看试题解析
9. x＝﹣ $\frac{1}{2}$ 是方程2x﹣1＝a+1的解，则（a+1）²的值为（　　）

A、 $\frac{1}{4}$ B、4 C、1 D、0

查看试题解析
10. 制作一件手工制品，如果由一个人完成需10小时，现在由一部分人先做1小时，再增加1人和他们一起做2小时，完成这项工作的 $\frac{4}{5}$ ，假设每个人的工作效率相同，具体先安排x人工作，则下列方程正确的是（　　）

A、 $\frac{x}{10}$ + $\frac{2 (x + 1)}{10}$ ＝1 B、 $\frac{x}{10}$ + $\frac{2 (x + 1)}{10}$ ＝ $\frac{4}{5}$ C、 $\frac{x}{10}$ ﹣ $\frac{2 (x - 1)}{10}$ ＝ $\frac{1}{5}$ D、 $\frac{x}{10}$ + $\frac{2 (x - 1)}{10}$ ＝ $\frac{4}{5}$

查看试题解析
11. 如图，在射线OA，OB，OC，OD，OE，OF所构成的图形中，∠AOB＝50°，图中锐角的个数为（　　）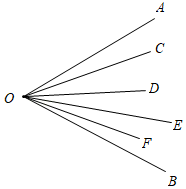

A、5个 B、10个 C、15个 D、16个

查看试题解析
12. 下列结论：①几个有理数相乘，若其中负因数有奇数个，则积为负；②两个三次多项式的和一定是三次多项式；③若xyz＜0，则 $\frac{| x |}{x}$ + $\frac{| y |}{y}$ + $\frac{| z |}{z}$ + $\frac{x y z}{| x y z |}$ 的值为0或﹣4；④若a，b互为相反数，则 $\frac{b}{a}$ ＝﹣1；⑤若x＝y，则 $\frac{x}{a^{2} + 1}$ ＝ $\frac{y}{a^{2} + 1}$ ．其中正确的个数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 如图，数轴上点A、B所表示的两个数的和是．

查看试题解析
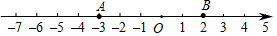14. 每年的5月31日为世界无烟日，开展无烟日活动旨在提醒世人吸烟有害健康，呼吁全世界吸烟者主动放弃吸烟，全世界每年因吸烟而引发疾病死亡的人数大约为5400000人，数据5400000人用科学记数法表示为．

查看试题解析
15. 若∠A＝21°36′，则∠A的余角为．

查看试题解析
16. 如图，这是一个数值转换机的示意图．若输入x的值为﹣2，输出的结果为4，则输入y的值为．

查看试题解析
17. 小明在做整式运算时，把一个多项式减去2ab﹣3bc+4误看成加上这个式子，得到的答案是4ab+2bc+1，则正确答案是．

查看试题解析
18. 定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数），并且运算重复进行，例如，取n＝26，第三次“F运算”的结果是11．若n＝111，则第2019次“F运算”的结果是．

查看试题解析

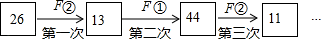
三、解答题

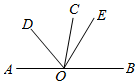
19. 计算：

(1)、（-3）×4+28÷（-7）．

(2)、|-9|÷3+（ $\frac{1}{2}$ - $\frac{1}{3}$ ）×12-（-2）² ．

查看试题解析
20. 解方程： $\frac{2 x - 3}{2}$ ﹣ $\frac{x - 6}{6}$ ＝1+ $\frac{1 - 3 x}{3}$

查看试题解析
21. 先化简，再求值：5（3x²y﹣xy²）﹣（xy²+3x²y）+6xy² ，其中x＝ $\frac{1}{2}$ ，y＝ $\frac{1}{3}$ ．

查看试题解析
22. 为响应国家节能减排的倡议，某汽车专卖店销售A、B两种型号的新能源汽车，B型汽车的售价比A型汽车售价高8万元，本周售出1辆A型车和3辆B型车，销售总额为96万元．

(1)、求每辆A型车和B型车的售价；

(2)、随着汽车限购政策的推行，预计下周起A，B两种型号的汽车价格在原有的基础上均有上涨，若A型汽车价格上涨m%，B型汽车价格上涨3m%，则同时购买了一台A型车和一台B型车需48.8万元，请用方程的知识求m的值．

查看试题解析
23. 如图，点A、O、B在同一条直线上，∠BOE＝60°，OD平分∠AOC，∠DOE＝3∠COE，求∠BOC的度数．

查看试题解析
24. 李阿姨逛街时发现．大润发超市和永辉超市有如下促销活动（两超市相同商品标价相同）：
大润发：所有商品打8.8折；

永辉：消费总金额不超过100元时，不打折；

消费总金额超过100元，不超过300元时，打9折；

消费总金额超过300元时，300元部分打9折，超出300元部分打8折．

(1)、李阿姨购买多少元的商品时，两个超市实际付款一样多？

(2)、活动期间李阿姨在永辉超市购买了两次商品，第一次实付款99元，第二次实付款286元，请问李阿姨两次购买商品的总价共为多少元？

查看试题解析
25. 如图，把一个边长为a的正方形分成9个完全相同的小正方形，把最中间的一个小正方形涂成白色（图①），再对其他8个小正方形作同样的分割（分成9个完全相同的小正方形，把最中间的一个小正方形涂成白色（图②），继续同样的方法分割图形（图③），…得到一些既复杂又漂亮的图形，它的每一部分放大，都和整体一模一样，它是波兰数学家谢尔宾斯基构造的，也被称为“谢尔宾斯基地毯”．求：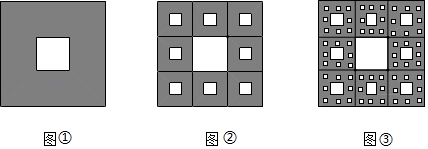

(1)、图③中最新的一个最小正方形的边长；

(2)、图③中所有涂黑部分的面积．

查看试题解析
26. 如图，在数轴上点A表示数a，点B表示数b，a、b满足|a﹣20|+（b+10）²＝0，O是数轴原点，点Q从点B出发，以每秒3个单位长度的速度沿数轴正方向匀速运动，设运动时间为t秒．

(1)、点A表示的数为，点B表示的数为．

(2)、t为何值时，BQ＝2AQ．

(3)、若在点Q从点B出发的同时，点P从点O出发，以每秒2个单位长度的速度一直沿数轴正方向匀速运动，而点Q运动到点A时，立即改变运动方向，沿数轴的负方向运动，到达点B时停止运动，在点Q的整个运动过程中，是否存在合适的t值，使得PQ＝6？若存在，求出所有符合条件的t值，若不存在，请说明理由．

查看试题解析