湖北省武汉市武昌区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 四个有理数 ,其中最小的是( )A、 B、 C、0 D、12. 一个数和它的相反数相等,则这个数是( )A、0 B、1 C、-1 D、3. 中国设计并制造的“神威·太湖之光”是世界上首台峰值运算速度超过每秒十亿亿次的超级计算机,其核心是完全由中国自主研发的40960块高性能处理器.40960用科学记数法表示为( )A、 B、 C、 D、4. 如图是由若干个相同的小正方体搭成的几何体,从上面看这个几何体,得到的平面图形是( )
 A、
A、 B、
B、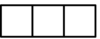 C、
C、 D、
D、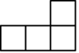 5. 下列说法正确的是( )A、 的系数是2 B、 的次数是1次 C、 是多项式 D、 的常数项为26. 如果 是方程 的解,则a的值为( )A、1 B、-1 C、2 D、-27. 下列运算中正确的是( )A、 B、 C、 D、8. 我国古代有一问题:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?如果设快马x天可追上慢马,下面所列方程中正确的是( )A、 B、 C、 D、9. 有理数m,n在数轴上的位置如图所示,化简 的结果为( )
5. 下列说法正确的是( )A、 的系数是2 B、 的次数是1次 C、 是多项式 D、 的常数项为26. 如果 是方程 的解,则a的值为( )A、1 B、-1 C、2 D、-27. 下列运算中正确的是( )A、 B、 C、 D、8. 我国古代有一问题:跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,快马几天可以追上慢马?如果设快马x天可追上慢马,下面所列方程中正确的是( )A、 B、 C、 D、9. 有理数m,n在数轴上的位置如图所示,化简 的结果为( ) A、2n B、-2n C、2m D、-2m10. 如图,D、E顺次为线段AB上的两点,AB=19,BE-DE=7,C为AD的中点,则AE-AC的值为( )
A、2n B、-2n C、2m D、-2m10. 如图,D、E顺次为线段AB上的两点,AB=19,BE-DE=7,C为AD的中点,则AE-AC的值为( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
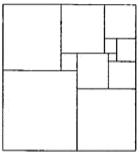
11. 比-3℃低6℃的温度是℃12. °.13. 如果 与 是同类项,则 的值为.14. 若一个角的补角比它的余角的 还多55°,则这个角为°.15. 点A、B、C在直线l上,AB=2BC,M、N分别为线段AB、BC的三等分点,BM= ,BN= ,则 .16. 如图,将一个正方形分割成11个大小不同的正方形,记图中最大正方形的周长是 ,最小正方形的周长是 ,则 .
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:
(1)、3x+7=32-2x(2)、19. 先化简,再求值: ,其中 .20. 某校七年级(1)(2)(3)(4)四个班的学生在植树节这天共植树 棵.其中(1)班植树x棵,(2)班植树的棵数比(1)班的2倍少40棵,(3)班植树的棵数比(2)班的一半多30棵,(1)、求(1)(2)(3)班共植树多少棵?(用含x的式子表示)(2)、若 ,求(4)班植树多少棵?21. 如图,点O在直线AB上,∠BOD与∠COD互补,∠BOC=3∠EOC (1)、若∠AOD=24°,则∠DOE的度数为.(2)、若∠AOD+∠BOE=110°,求∠AOD的度数.22. 公园门票价格规定如下表:
(1)、若∠AOD=24°,则∠DOE的度数为.(2)、若∠AOD+∠BOE=110°,求∠AOD的度数.22. 公园门票价格规定如下表:购票张数
1~50张
51~100张
100张以上
每张票的价格
15元
13元
11元
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)、两个班各有多少学生?(2)、如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?(3)、如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?23. 已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧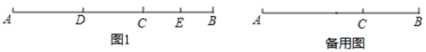 (1)、若AB=18,DE=8,线段DE在线段AB上移动
(1)、若AB=18,DE=8,线段DE在线段AB上移动①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)、若AB=2DE,线段DE在直线AB上移动,且满足关系式 ,则 .24. 已知∠AOB=120°,∠COD=40°,OM平分∠AOC,ON平分∠BOD(图中的角均大于0°且小于180°)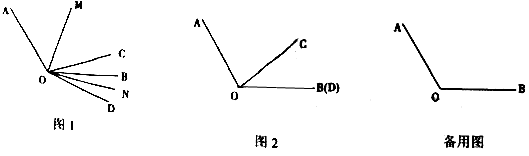 (1)、如图1,求∠MON的度数;(2)、若OD与OB重合,OC从图2中的位置出发绕点O逆时针以每秒10°的速度旋转,同时OD从OB的位置出发绕点O顺时针以每秒5°的速度旋转,旋转时间为t秒
(1)、如图1,求∠MON的度数;(2)、若OD与OB重合,OC从图2中的位置出发绕点O逆时针以每秒10°的速度旋转,同时OD从OB的位置出发绕点O顺时针以每秒5°的速度旋转,旋转时间为t秒①当 时,试确定∠BOM与∠AON的数量关系;
②当 且 时,若 ,则t=.