河南省南阳市南召县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 的相反数是( )A、2 B、 C、 D、2. 据海关统计,今年第一季度我国外贸进出口总额是70100亿元人民币,比去年同期增长了3.7%,数70100亿用科学记数法表示为( )A、7.01×104 B、7.01×1011 C、7.01×1012 D、7.01×10133. 下面运算正确的是( )A、3a+6b=9ab B、8a4-6a3=2a C、 D、3a2b-3ba2=04. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是( )
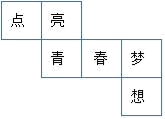 A、青 B、春 C、梦 D、想5. 如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )
A、青 B、春 C、梦 D、想5. 如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( ) A、50° B、45° C、30° D、40°6. 单项式 的系数是( )A、-2 B、 C、3 D、7. 如图,已知 , , 平分 , 平分 ,则 的度数是( )
A、50° B、45° C、30° D、40°6. 单项式 的系数是( )A、-2 B、 C、3 D、7. 如图,已知 , , 平分 , 平分 ,则 的度数是( )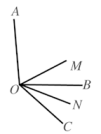 A、 B、 C、 D、8. 如图, , , 是线段 上的三个点,下面关于线段 的表示:① ;② ;③ ;④ .其中正确的是( )
A、 B、 C、 D、8. 如图, , , 是线段 上的三个点,下面关于线段 的表示:① ;② ;③ ;④ .其中正确的是( )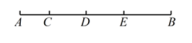 A、①②③④ B、①② C、①②④ D、②③④9. 如图,一副直角三角板按如图所示的方式摆放,其中点 在 的延长线上,且AB∥FC,则 的度数为( )
A、①②③④ B、①② C、①②④ D、②③④9. 如图,一副直角三角板按如图所示的方式摆放,其中点 在 的延长线上,且AB∥FC,则 的度数为( ) A、15° B、30° C、45° D、60°10. 若|m|=5,|n|=7,m+n<0,则m﹣n的值是( )A、﹣12或﹣2 B、﹣2或12 C、12或2 D、2或﹣12
A、15° B、30° C、45° D、60°10. 若|m|=5,|n|=7,m+n<0,则m﹣n的值是( )A、﹣12或﹣2 B、﹣2或12 C、12或2 D、2或﹣12二、填空题
-
11. 计算: ;12. 写出一个只含有字母 的二次三项式(写出一个即可).13. 若锐角 ,那么锐角 余角的补角为 .14. 如图,写出一个能判定EC∥AB的条件是 .
 15. 计算: .
15. 计算: .三、解答题
-
16. 计算:17. 计算:-1-18.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的平面图形.
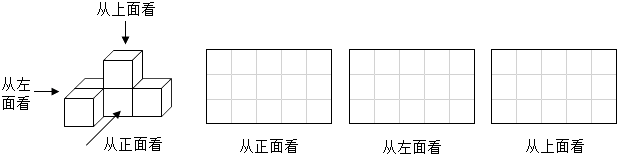 19. 设 , .(1)、化简: .(2)、若 ,求 值.20. 如图,已知直线AB∥CD,直线 分别交 , 于 , 两点,若 , 分别是 , 的角平分线,试说明:ME∥NF.
19. 设 , .(1)、化简: .(2)、若 ,求 值.20. 如图,已知直线AB∥CD,直线 分别交 , 于 , 两点,若 , 分别是 , 的角平分线,试说明:ME∥NF.
解:∵AB∥CD,(已知)
∴ ,
∵ , 分别是 , 的角平分线,(已知)
∴∠EMN=∠AMN,
∠FNM=∠DNM,(角平分线的定义)
∴ ,(等量代换)
∴ME∥NF,
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对角的平分线互相 .
21. 某电器商销售一种微波炉和电磁炉,微波炉每台定价800元,电磁炉每台定价200元.“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的90%付款.
现某客户要到该卖场购买微波炉10台,电磁炉x台(x>10).
(1)、若该客户按方案一购买,需付款元.(用含x的代数式表示)若该客户按方案二购买,需付款元.(用含x的代数式表示)(2)、若x=30,通过计算说明此时按哪种方案购买较为合算?(3)、当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.并计算需付款多少元?22. 已知: 为直线 上的一点,以 为观察中心,射线 表示正北方向, 表示正东方向(即 ),射线 ,射线 的方向如各图所示.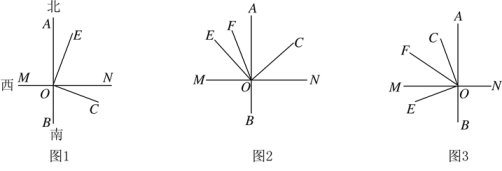 (1)、如图1所示,当 时:
(1)、如图1所示,当 时:①若 ,则射线 的方向是 .
② 与 的关系为 ,
③ 与 的关系为 .
(2)、若将射线 ,射线 绕点 旋转至图 的位置,另一条射线 恰好平分 ,旋转中始终保持 .①若 ,则 度.
②若 ,则 (用含 的代数式表示).
(3)、若将射线 ,射线 绕点 旋转至图 的位置,射线 仍然平分 ,旋转中始终保持 ,则 与 之间存在怎样的数量关系,并说明理由.23. 问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)、数学活动小组经过讨论形成下列推理,请你补全推理依据.如图2,过点P作PE∥AB,
∵PE∥AB(作图知)
又∵AB∥CD,
∴PE∥CD.
∴∠A+∠APE=180°.
∠C+∠CPE=180°.
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
(2)、如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.(3)、在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系.