江苏省扬州市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 2018年是改革开放40周年，四十年春华秋实，改革开放波澜壮阔，这是一个伟大的时代，据报道：我市2018年城乡居民人均可支配收入达到34534元，迈上新台阶，将34534用科学记数法表示为（）

A、 3.4534×10⁴ B、3.4534×10⁵ C、3.4534×10³ D、34.534×10³

查看试题解析
2. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 若数a，b在数轴上的位置如图示，则（）

A、a+b＞0 B、ab＞0 C、a﹣b＞0 D、﹣a﹣b＞0

查看试题解析
4. 下列生活实例中，数学原理解释错误的一项是（）

A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线 B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短 C、把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线 D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短

查看试题解析
5. 为了贯彻“房住不炒”要求，加快回笼资金，我市甲、乙、丙三家原售价相同的楼盘在年终前搞促销活动，甲楼盘售楼处打出在原价基础上先降价15%，再降价15%；乙楼盘打出一次性降价30%；丙楼盘打出先九折，再降价20%，如果此时小容的父亲想在上述三家楼盘中选择每平米实际售价最低的一处购买，他应选择的楼盘是（）

A、甲 B、乙 C、丙 D、都一样

查看试题解析
6. 如图，点O在直线DB上，OA⊥OC，∠1＝20°，则∠2的度数为（）

A、150° B、120° C、110° D、100°

查看试题解析
7. 一张长方形纸片的长为m，宽为n（m＞3n）如图1，先在其两端分别折出两个正方形（ABEF、CDGH）后展开（如图2），再分别将长方形ABHG、CDFE对折，折痕分别为MN、PQ（如图3），则长方形MNQP的面积为（　　）

A、n² B、n（m﹣n） C、n（m﹣2n） D、

查看试题解析

二、填空题

8. $- \frac{1}{2}$ 的相反数是．

查看试题解析
9. 单项式- $\frac{2 {xy}^{2}}{5}$ 的系数是.

查看试题解析
10. 已知 $x = 1$ 是关于 $x$ 的方程 $2 x - m = 3$ 的解，则代数式 $m$ = ．

查看试题解析
11. 若a﹣2b+3＝0，则2019﹣a+2b＝.

查看试题解析
12. 若代数式﹣（3x³y^m﹣1）+3（xⁿy+1）经过化简后的结果等于4，则m﹣n的值是.

查看试题解析
13. 如果关于x的方程 $2 x + 1 = 3$ 和方程 $2 - \frac{a - x}{3} = 1$ 的解相同，那么a的值为.

查看试题解析
14. 如图，一个宽度相等的纸条按如图所示方法折叠压平，则∠1的度数等于°.

查看试题解析
15. 一组“数值转换机”按下面的程序计算，如果输入的数是30，则输出的结果为56，要使输出的结果为60，则输入的最小正整数是.

查看试题解析
16. 由5个棱长为1的小正方形组成的几何体如图放置，一面着地，两面靠墙，如果要将露出来的部分涂色，则涂色部分的面积为.

查看试题解析
17. 120°24′﹣60.6°＝°.

查看试题解析
18. 计算： $- 2 - | - 3 |$ = ．

查看试题解析
19. 已知关于 $x$ 的一元一次方程 $\frac{x}{2019} + 3 = 2019 x + m$ 的解为 $x = 2$ ，那么关于 $x$ 的一元二次方程 $\frac{1 - y}{2019} + 2019 (y - 1) = m - 3$ 的解 $y$ = ．

查看试题解析

三、解答题

20. 计算：

(1)、﹣3²÷（﹣3）²+3×（﹣2）+|﹣4|；

(2)、66× $(- \frac{1}{2} - \frac{1}{3} \times \frac{7}{11})$ .

查看试题解析
21. 解方程：

(1)、4（x﹣2）＝2﹣x；

(2)、 $\frac{3 y + 1}{4} = 2 - \frac{2 y - 1}{3}$ .

查看试题解析
22. 化简与求值：
先化简2（3xy﹣x²）﹣3（xy﹣2x²）﹣xy，并求当|x+3|+（y﹣2）²＝0时原式的值.

查看试题解析
23. 如图，点C是线段AB上一点，点D是线段AC的中点，若BC比AC长1cm，BD=4.6cm，求BC的长．

查看试题解析
24. 画图，探究：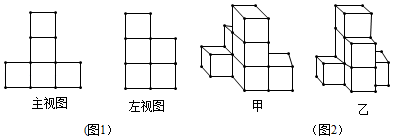

(1)、一个正方体组合图形的主视图、左视图（如图1）所示．
①这个几何体可能是（图2）甲、乙中的；

②这个几何体最多可由个小正方体构成，请在图3中画出符合最多情况的一个俯视图．

(2)、如图，已知一平面内的四个点A、B、C、D，根据要求用直尺画图．
①画线段AB，射线AD；

②找一点M，使M点即在射线AD上，又在直线BC上；

③找一点N，使N到A、B、C、D四个点的距离和最短．

查看试题解析
25. 某校组织部分师生从学校（A地）到300千米外的B地进行红色之旅（革命传统教育），租用了客运公司甲、乙两辆车，其中乙车速度是甲车速度的 $\frac{4}{5}$ ，两车同时从学校出发，以各自的速度匀速行驶，行驶2小时后甲车到达服务区C地，此时两车相距40千米，甲车在服务区休息15分钟户按原速度开往B地，乙车行驶过程中未做停留.

(1)、求甲、乙两车的速度？

(2)、问甲车在C地结束休息后再行驶多长时间，甲、乙两车相距30千米？

查看试题解析
26. 如图，直线AB与CD相交于点E，射线EG在∠AEC内(如图1).

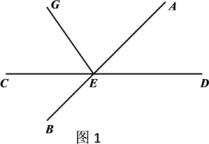
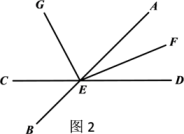(1)、若∠BEC的补角是它的余角的3倍，则∠BEC=度；

(2)、在（1）的条件下，若∠CEG比∠AEG小25度，求∠AEG的大小；

(3)、若射线EF平分∠AED，∠FEG=100°（如图2），则∠AEG－∠CEG=度.

查看试题解析
27. 有两个大小完全一样长方形OABC和EFGH重合着放在一起，边OA、EF在数轴上， O为数轴原点（如图1），长方形OABC的边长OA的长为6个坐标单位．

(1)、数轴上点A表示的数为．

(2)、将长方形EFGH沿数轴所在直线水平移动．
①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的一半时，则移动后点F在数轴上表示的数为．

②若长方形EFGH向左水平移动后，D为线段AF的中点，求当长方形EFGH移动距离x为何值时，D、E两点在数轴上表示的数时互为相反数？

查看试题解析