山东省临沂市兰陵县2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 用配方法解一元二次方程 时,此方程可变形为( )A、 B、 C、 D、2. 共享单车为市民出行带来了方便,某单车公司第一季度投放1万辆单车,计划第三季度投放单车的数量比第一季度多4400辆,设该公司第二、三季度投放单车数量的平均增长率均为 ,则所列方程正确是( )A、 B、 C、 D、3. 在平面直角坐标系中,平移二次函数y=x2+4x+3的图象能够与二次函数y=x2的图象重合,则平移方式为( )A、向左平移2个单位,向下平移1个单位 B、向左平移2个单位,向上平移1个单位 C、向右平移2个单位,向下平移1个单位 D、向右平移2个单位,向上平移1个单位4. 已知反比例函数y=﹣ ,下列结论中错误的是( )A、函数图象经过点(﹣3,2) B、函数图象分别位于第二、四象限 C、若x<﹣2,则0<y<3 D、y随x的增大而增大5. 相同方向行驶的两辆汽车经过同一个“T”形路口时,可能向左转或向右转.如果这两种可能性大小相同,则这两辆汽车经过该路口时,都向右转的概率是( )A、 B、 C、 D、6. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=90°,则∠BCD的度数是( )
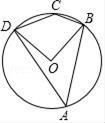 A、45° B、90° C、135° D、150°7. 如图,⊙O是△ABC的外接圆,BC=3,∠BAC=30°,则劣弧 的长等于( )
A、45° B、90° C、135° D、150°7. 如图,⊙O是△ABC的外接圆,BC=3,∠BAC=30°,则劣弧 的长等于( ) A、 B、π C、 D、 π8. 如图,DE∥BC,CD与BE相交于点O,若 ,则 的值为( )
A、 B、π C、 D、 π8. 如图,DE∥BC,CD与BE相交于点O,若 ,则 的值为( ) A、 B、 C、 D、9. 对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是( )A、开口向下 B、对称轴是直线x=﹣2 C、x>﹣2时,y随x的增大而增大 D、x=﹣2,函数有最大值y=﹣110. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确是( )
A、 B、 C、 D、9. 对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是( )A、开口向下 B、对称轴是直线x=﹣2 C、x>﹣2时,y随x的增大而增大 D、x=﹣2,函数有最大值y=﹣110. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确是( )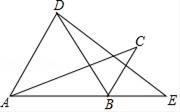 A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC11. 如图,在△ABC中, ∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,连接C′C,使得C′C∥AB,则∠BAB′=( )
A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC11. 如图,在△ABC中, ∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,连接C′C,使得C′C∥AB,则∠BAB′=( ) A、 B、 C、 D、12. 如图,在平面直角坐标系中,点 是函数 图象上的点,过点 作 轴的垂线交 轴于点 ,点 在 轴上,若 的面积为1,则 的值为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,点 是函数 图象上的点,过点 作 轴的垂线交 轴于点 ,点 在 轴上,若 的面积为1,则 的值为( )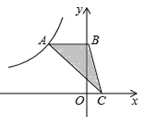 A、1 B、2 C、 D、13. 如图,点 、 、 在圆 上,若 , ,则图中阴影部分的面积是( )
A、1 B、2 C、 D、13. 如图,点 、 、 在圆 上,若 , ,则图中阴影部分的面积是( ) A、 B、 C、 D、14. 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( )
A、 B、 C、 D、14. 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( ) A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m C、小球从飞出到落地要用时4s D、小球飞出1s时的飞行高度为10m
A、小球的飞行高度不能达到15m B、小球的飞行高度可以达到25m C、小球从飞出到落地要用时4s D、小球飞出1s时的飞行高度为10m二、填空题
-
15. 有5张看上去无差别的卡片,正面分别写着1,2,3,4,5,洗匀后正面向下放在桌子上,从中随机抽取2张,抽出的卡片上的数字恰好是两个连续整数的概率是 .16. 若二次函数 的图象与 轴有两个不相同的交点,则 的取值范围是 .17. 利用标杆 测量建筑物的高度的示意图如图所示,若标杆 的高为 米,测得 米, 米,则建筑物的高 为米.
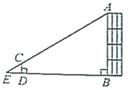 18. 如图,过原点 的直线与反比例函数的图象相交于点 、 ,根据图中提供的信息可知,这个反比例函数的解析式为 .
18. 如图,过原点 的直线与反比例函数的图象相交于点 、 ,根据图中提供的信息可知,这个反比例函数的解析式为 .
三、解答题
-
19. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数 , ,2, 4.(1)、摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为 .(2)、摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.20. 如图,已知 是 外一点, 交 于点 , ,弦 ,劣弧 所对的圆周角度数为 ,连接 .
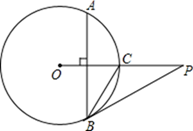 (1)、求 的长;(2)、求证: 是 的切线.21. 如图,点 是正方形 的边 上一点,把 顺时针旋转到 的位置.
(1)、求 的长;(2)、求证: 是 的切线.21. 如图,点 是正方形 的边 上一点,把 顺时针旋转到 的位置. (1)、连结 ,试判断 的形状;(2)、若四边形 的面积为36, ,求 的长.22. 制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.
(1)、连结 ,试判断 的形状;(2)、若四边形 的面积为36, ,求 的长.22. 制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.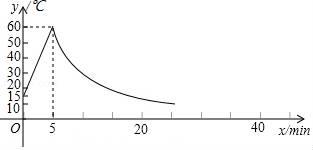 (1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?23. 如图,二次函数y= x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?23. 如图,二次函数y= x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6). (1)、求二次函数的解析式;(2)、求函数图象的顶点坐标及D点的坐标;(3)、二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
(1)、求二次函数的解析式;(2)、求函数图象的顶点坐标及D点的坐标;(3)、二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.