山东省泰安市泰山区2018-2019学九年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 如图所示,该几何体的左视图是( )
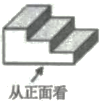 A、
A、 B、
B、 C、
C、 D、
D、 2. 在 中, ,则 的度数是( )
2. 在 中, ,则 的度数是( )A.30° B.45° C.60° D.90°
A、30° B、45° C、60° D、90°3. 反比例函数 具有的性质是( )A、当 时, B、在每个象限内, 随 的增大而减小 C、图象分布在第二、四象限 D、图象分布在第一、三象限4. 一个不透明的口袋中装有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸出一个小球后不放回,再随机摸出一个小球,则两次摸出的小球标号之和等于6的概率为( )A、 B、 C、 D、5. 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )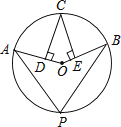 A、140° B、70° C、60° D、40°6. 抛物线 可以由抛物线 平移而得到,下列平移正确是( )A、先向左平移3个单位长度,然后向下平移2个单位长度 B、先向左平移3个单位长度,然后向上平移2个单位长度 C、先向右平移3个单位长度,然后向下平移2个单位长度 D、先向右平移3个单位长度,然后向上平移2个单位长度7. 如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形,它们分别是△P1A1O、△P2A2O、△P3A30,设它们的面积分别是S1、S2、S3 , 则( )
A、140° B、70° C、60° D、40°6. 抛物线 可以由抛物线 平移而得到,下列平移正确是( )A、先向左平移3个单位长度,然后向下平移2个单位长度 B、先向左平移3个单位长度,然后向上平移2个单位长度 C、先向右平移3个单位长度,然后向下平移2个单位长度 D、先向右平移3个单位长度,然后向上平移2个单位长度7. 如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形,它们分别是△P1A1O、△P2A2O、△P3A30,设它们的面积分别是S1、S2、S3 , 则( )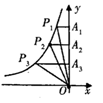 A、S1<S2<S3 B、S2<S1<S3 C、S3<S1<S2 D、S1=S2 =S38. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、
A、S1<S2<S3 B、S2<S1<S3 C、S3<S1<S2 D、S1=S2 =S38. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、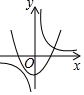 B、
B、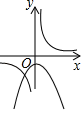 C、
C、 D、
D、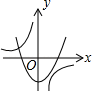 9. 关于二次函数y=2x2+4x-3,下列说法正确是( )A、图象与 轴的交点坐标为 B、图象的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-510. 如图,⊙A过点O(0,0),C( ,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )
9. 关于二次函数y=2x2+4x-3,下列说法正确是( )A、图象与 轴的交点坐标为 B、图象的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-510. 如图,⊙A过点O(0,0),C( ,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是( )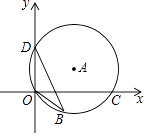 A、15° B、30° C、45° D、60°11. 如图,扇形纸扇完全打开后,扇形ABC的面积为 ,∠BAC=150°,BD=2AD,则 的长度为( )
A、15° B、30° C、45° D、60°11. 如图,扇形纸扇完全打开后,扇形ABC的面积为 ,∠BAC=150°,BD=2AD,则 的长度为( ) A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确个数是( )
A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .14. 若函数 与 的图象有一个交点坐标是 ,则另一个交点坐标是.15. 如图,在“ ”网格中,有 个涂成黑色的小方格.若再从余下的 个小方格中随机选取 个涂成黑色,则完成的图案为轴对称图案的概率是 .
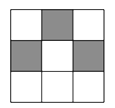 16. 若一个等腰三角形的两边长分别为 和 ,则底角的正切值为.17. 工人师傅用一张半径为 ,圆心角为120°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为.18. 二次函数 的图象如图所示,以下结论:① ;②顶点坐标为 ;③ ;④ ;⑤ .正确有.(填序号)
16. 若一个等腰三角形的两边长分别为 和 ,则底角的正切值为.17. 工人师傅用一张半径为 ,圆心角为120°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为.18. 二次函数 的图象如图所示,以下结论:① ;②顶点坐标为 ;③ ;④ ;⑤ .正确有.(填序号)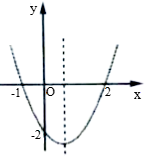
三、解答题
-
19. 为调查达州市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
 (1)、本次调查中,一共调查了名市民;扇形统计图中,B项对应的扇形圆心角是度;补全条形统计图;(2)、若甲、乙两人上班时从A,B,C,D四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.20. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于A(﹣2,1),B(1,n)两点.
(1)、本次调查中,一共调查了名市民;扇形统计图中,B项对应的扇形圆心角是度;补全条形统计图;(2)、若甲、乙两人上班时从A,B,C,D四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.20. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于A(﹣2,1),B(1,n)两点. (1)、求反比例函数和一次函数的解析式;(2)、根据图象写出一次函数的值大于反比例函数的值的x的取值范围.21. 如图,是我国跨度最大的公路和铁路两用桥梁引申出的部分平面图,测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果保留根号)
(1)、求反比例函数和一次函数的解析式;(2)、根据图象写出一次函数的值大于反比例函数的值的x的取值范围.21. 如图,是我国跨度最大的公路和铁路两用桥梁引申出的部分平面图,测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果保留根号)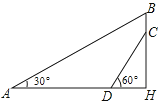 22. 如图,在平面直角坐标系 中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧), ,△ADC与△ABC关于AC所在的直线对称.
22. 如图,在平面直角坐标系 中,已知△ABC,∠ABC=90°,顶点A在第一象限,顶点B、C在x轴的正半轴上(C在B的右侧), ,△ADC与△ABC关于AC所在的直线对称.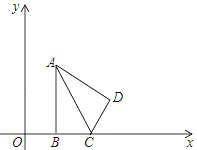 (1)、当OB=2时,求点D的坐标.(2)、若点 和点 在同一个反比例函数图象上,求 的长.23. 已知函数 .(1)、求证:不论 为何实数,此二次函数的图象与 轴都有两个不同交点.(2)、若函数有最小值 ,求函数表达式.24. 如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 ,连结 ,已知 .
(1)、当OB=2时,求点D的坐标.(2)、若点 和点 在同一个反比例函数图象上,求 的长.23. 已知函数 .(1)、求证:不论 为何实数,此二次函数的图象与 轴都有两个不同交点.(2)、若函数有最小值 ,求函数表达式.24. 如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 ,连结 ,已知 . (1)、求证: 是 的切线.(2)、若 ,求 的半径.25. 如图1,在平面直角坐标系中,直线 与抛物线 交于 两点,其中 , .该抛物线与 轴交于点 ,与 轴交于另一点 .
(1)、求证: 是 的切线.(2)、若 ,求 的半径.25. 如图1,在平面直角坐标系中,直线 与抛物线 交于 两点,其中 , .该抛物线与 轴交于点 ,与 轴交于另一点 .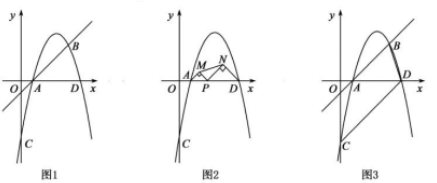 (1)、求 的值及该抛物线的解析式;(2)、如图2.若点 为线段 上的一动点(不与 重合).分别以 、 为斜边,在直线 的同侧作等腰直角△ 和等腰直角△ ,连接 ,试确定△ 面积最大时 点的坐标.(3)、如图3.连接 、 ,在线段 上是否存在点 ,使得以 为顶点的三角形与△ 相似,若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求 的值及该抛物线的解析式;(2)、如图2.若点 为线段 上的一动点(不与 重合).分别以 、 为斜边,在直线 的同侧作等腰直角△ 和等腰直角△ ,连接 ,试确定△ 面积最大时 点的坐标.(3)、如图3.连接 、 ,在线段 上是否存在点 ,使得以 为顶点的三角形与△ 相似,若存在,请直接写出点 的坐标;若不存在,请说明理由.