湖南省株洲市醴陵市2019-2020学年九年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 2 x = 0$ 的解为（）

A、 $x_{1} = x_{2} = 2$ B、 $x_{1} = 0$ ， $x_{2} = 2$ C、 $x_{1} = 0$ ， $x_{2} = - 2$ D、 $x_{1} = x_{2} = 0$

查看试题解析
2. 用配方法解一元二次方程x²﹣4x=5时，下列配方正确的是（　　）

A、（x﹣2）²=9 B、（x﹣2）²=1 C、（x+2）²=9 D、（x+2）²=1

查看试题解析
3. 下列各组图形一定相似的是（）

A、两个直角三角形 B、两个等边三角形 C、两个菱形 D、两个矩形

查看试题解析
4. 若 $\frac{x}{y}$ ＝ $\frac{2}{3}$ ，则下列各式不成立的是（）

A、 $\frac{x + y}{y}$ ＝ $\frac{5}{3}$ B、 $\frac{y - x}{y}$ ＝ $\frac{1}{3}$ C、 $\frac{x}{2 y}$ ＝ $\frac{1}{3}$ D、 $\frac{x + 1}{y + 1}$ ＝ $\frac{3}{4}$

查看试题解析
5. 如图，E是平行四边形ABCD的边BA延长线上的一点，CE交AD于点F，下列各式中不正确的是（）

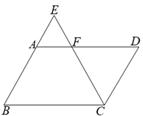A、 $\frac{A E}{A B} = \frac{E F}{C F}$ B、 $\frac{A E}{B E} = \frac{E F}{C E}$ C、 $\frac{A E}{A B} = \frac{A F}{B C}$ D、 $\frac{A E}{A B} = \frac{A F}{D F}$

查看试题解析
6. 如图，有一斜坡 $AB$ ，坡顶B离地面的高度BC为30m，斜坡AB的坡度为1：2，则此斜坡AB为（）

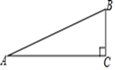A、 $30 \sqrt{5}$ m B、60m C、30m D、15m

查看试题解析
7. 如果∠ $α$ 为锐角，且sin $α$ ＝0.6，那么 $α$ 的取值范围是（）

A、0°＜ $α$ ≤30° B、30°＜ $α$ ＜45° C、45°＜ $α$ ＜60° D、60°＜ $α$ ≤90°

查看试题解析
8. 在锐角 $△ A B C$ 中， ${(\tan C - \sqrt{3})}^{2} + | \sqrt{2} - 2 \sin B | = 0$ ，则 $∠ A =$ （）

A、30° B、45° C、60° D、75°

查看试题解析
9. 已知原点是抛物线y＝(m＋1)x²的最高点，则m的范围是（）

A、m＜－1 B、m＜1 C、m＞－1 D、m＞－2

查看试题解析
10. 已知二次函数y=ax²+bx+c（ $a \neq 0$ ）的图像如图所示，则下列结论：（1）ac>0；（2）方程ax²+bx+c=0的两根之积小于0；（3）a+b+c<0；（4）ac+b+1 <0，其中符合题意的个数（）

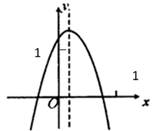A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 有两个的实数根。（填“相等”或“不相等”）

查看试题解析
12. 已知 $x : y : z = 1 : 3 : 5$ ，则 $\frac{x + 3 y - z}{x - 3 y + z}$ 的值是．

查看试题解析
13. 直角三角形在正方形网格纸中的位置如图所示，则 $\cos α$ =.

查看试题解析
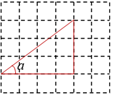14. 如图，AB//CD， $∠ B = 90 °$ ，E为BC上一点，且 $A E ⊥ E D$ ．若 $A B = 3$ ， $B E = 4$ ， $D C = 6$ ，则DE的长为．

查看试题解析
15. 抛物线 $y = 2 (x - 3) (x - 1)$ 的顶点坐标是．

查看试题解析
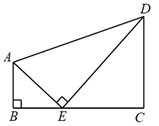16. 某中学共有学生 $4600$ 人，为了解学生最喜欢的课外体育运动项目的情况，学校随机抽查了200名学生，其中有 $85$ 名学生表示最喜欢的项目是跳绳，则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有人．

查看试题解析
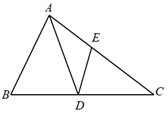17. 如图，在 $△ A B C$ 中，D是BC边上一点，且满足 $A D = A B$ ， $∠ A D E = ∠ C$ ，若 $\frac{S_{△ A D E}}{S_{△ C D E}} = \frac{2}{3}$ ，且 $A E = 2$ ，则AB的长为．

查看试题解析
18. 关于x的方程（a﹣6）x²﹣8x+6=0有实数根，则整数a的最大值是．

查看试题解析

三、解答题

19.

(1)、计算： $2^{2} - 2 \sin 30 ° + \tan 45 °$

(2)、解方程：x²-2x-2=0.

查看试题解析
20. 某中学为了了解本校学生喜爱的球类运动，在本校范围内随机抽查了部分学生，将收集的数据统计整理，绘制成如下两幅不完整的统计图．

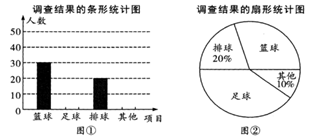
请你根据图中提供的信息解答下列问题：

(1)、本次一共调查了名学生；

(2)、补全条形统计图；

(3)、“足球”在扇形统计图中所占圆心角的度数为；

(4)、若已知该校有1000名学生，请你根据调查的结果估计爱好“足球”和“排球”的学生共有多少人？

查看试题解析
21. 如图，某办公楼AB的右边有一建筑物CD，在建设物CD离地面2米高的点E处观测办公楼顶A点，测得的仰角 $∠ A E M$ = $22 °$ ，在离建设物CD 25米远的F点观测办公楼顶A点，测得的仰角 $∠ A F B$ = $45 °$ （B，F，C在一条直线上）．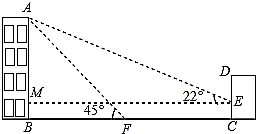

(1)、求办公楼AB的高度；

(2)、若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．（参考数据： $\sin 22^{°} = \frac{3}{8} ， \cos 22^{°} = \frac{15}{16} ， \tan 22^{°} = \frac{2}{5}$ ）

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - 2 x - a = 0$ .

(1)、如果此方程有两个不相等的实数根，求a的取值范围；

(2)、如果此方程的两个实数根为 $x_{1} ， x_{2}$ ，且满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - \frac{1}{3}$ ，求a的值.

查看试题解析
23. 如图， $△ A B C$ 中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上， $B C = 30$ ，BC边上的高 $A D = 20$ ，求S_正方形_EFGH ．

查看试题解析
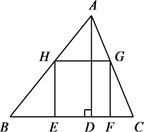24. 如图，点E是矩形ABCD中CD边上一点， $△ B C E$ 沿BE折叠为 $△ B F E$ ，点F落在AD上

(1)、求证： $△ A B F ∽ △ D F E$ ；

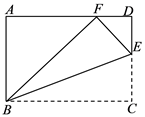(2)、若 $\sin ∠ D F E = \frac{2}{3}$ ，求 $\tan ∠ E B C$ 的值．

查看试题解析
25. 如图，若m是正数，直线l：y＝－m与y轴交于点A；直线a：y＝x+m与y轴交于点B；抛物线L：y＝ x²+mx的顶点为C，且L与x轴左交点为D．

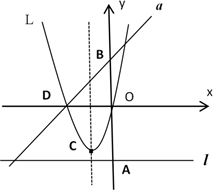(1)、若AB＝12，求m的值，此时在抛物线的对称轴上存在一点Ｐ使得△ $OBP$ 的周长最小，求点Ｐ坐标；

(2)、当点C在直线l上方时，求点C与直线l距离的最大值；

(3)、在抛物线L和直线a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出m＝2020和m＝2020.5时“美点”的个数．

查看试题解析