山东省济南市槐荫区2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. 在﹣4，2，﹣1，3这四个数中，比﹣2小的数是（）

A、﹣4 B、2 C、﹣1 D、3

查看试题解析
2.
如图所示的几何体是由五个小正方体组合而成的，它的主视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 2019 年 11 月 27 日下午槐荫区数学文化年闭幕式暨“槐荫区第二届‘勾股数学’杯初中校际联赛”隆重举行，全市各初中学校代表、家长代表、学生代表共计 500 人现场观摩了比赛，其中数字 500 用科学记数法可表示为（）

A、0.5´10⁴ B、5´10³ C、5´10² D、50 ´10

查看试题解析
4. 下列调查中，最适宜采用普查方式的是（）

A、对我国初中学生视力状况的调查 B、对量子科学通信卫星上某种零部件的调查 C、对一批节能灯管使用寿命的调查 D、对“最强大脑”节目收视率的调查

查看试题解析
5. 以下说法中正确是（）

A、延长射线 AB B、延长直线 AB C、画直线 AB 直线等于1cm D、延长线段 AB 到C

查看试题解析
6. 若-5a^2mb 与b³^-ⁿa⁴是同类项，则m+n=（）

A、2 B、3 C、4 D、6

查看试题解析
7. 若关于x的一元一次方程2x+a=4的解是x=3，则a的值是（）

A、2 B、-2 C、4 D、10

查看试题解析
8. 若a-b=1，则代数式2b-2a-3的值是（）

A、1 B、-1 C、5 D、-5

查看试题解析
9. 某品牌服装折扣店将某件衣服按进价提高50%后标价，再打8折（标价的80%）销售，售价为240元.设这件衣服的进价为 $x$ 元，根据题意，下面所列的方程正确是（）

A、 $x \cdot 50 % \times 80 % = 240$ B、 $x \cdot (1 + 50 %) \times 80 % = 240$ C、 $240 \times 50 % \times 80 % = x$ D、 $x \cdot (1 + 50 %) = 240 \times 80 %$

查看试题解析
10. 某校为开展第二课堂，组织调查了本校150名学生各自最喜爱的一项体育活动，制成了如下扇形统计图，则在该被调查的学生中，跑步和打羽毛球的学生人数分别是（）

A、30，40 B、45，60 C、30，60 D、45，40

查看试题解析
11. 如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（　　）

A、0°＜α＜90° B、α＝90° C、90°＜α＜180° D、α随折痕GF位置的变化而变化

查看试题解析
12. 已知整数 $a_{1} ， a_{2} ， a_{3} ， a_{4}$ …满足下列条件： $a_{1} = 0$ ， $a_{2} = - | a_{1} + 1 |$ ， $a_{3} = - | a_{2} + 2 |$ ， $a_{4} = - | a_{3} + 3 |$ …依次类推，则 $a_{2020}$ 的值为（）

A、-1007 B、-1009 C、-1010 D、-2020

查看试题解析

二、填空题

13. －6的相反数是．

查看试题解析
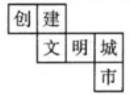
14. 单项式 $\frac{3 π a^{2} b^{4}}{5}$ 的系数是

查看试题解析
15. 如图，这是一个正方体的展开图，则原正方体中与“创”字所在的面相对的面上标的字是.

查看试题解析
16. 下午12:20 分，钟表上时针与分针所夹角的度数为度（所求夹角小于180°）．

查看试题解析
17. 已知 a 、b 、c 的位置如图：则 $| - a | - | c - b | - | a - c |$ =

查看试题解析
18. 一动点 P 从数轴上的原点出发，沿数轴的正方向以每前进 5 个单位，后退 3 个单位的程序运动，已知 P 每秒前进或后退 1 个单位，设 xn 表示第 n 秒点 P 在数轴的位置所对应的的数，例如x₄=4，x₅=5，x₆=4，则x₂₀₂₀=

查看试题解析

三、解答题

19. 计算：

(1)、(-3)×2+(-24)÷4-(-3)

(2)、(-3)²× $[- \frac{2}{3} + (- \frac{5}{9})]$

查看试题解析
20. 如图：线段 $A B = 14 c m$ ， $C$ 是 $A B$ 上一点，且 $A C = 9 c m$ ， $O$ 是 $A B$ 的中点，求线段 $O C$ 的长度．

查看试题解析
21.

(1)、化简：4a+2(a-b)

(2)、先化简，再求值 $9 a b - 6 b^{2} - 3 (a b - \frac{2}{3} b^{2})$ ，其中 $a = \frac{1}{2}, b = - 1$

查看试题解析
22.

(1)、解方程：3(x-4)=12

(2)、解方程: $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$

查看试题解析
23. 某一天，水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克，后再到水果市场去卖，已知猕猴桃和芒果当天的批发价和零售价如表所示：

品名

猕猴桃

芒果

批发价 $($ 元 $/$ 千克 $)$

20

40

零售价 $($ 元 $/$ 千克 $)$

26

50

(1)、他购进的猕猴桃和芒果各多少千克？

(2)、如果猕猴桃和芒果全部卖完，他能赚多少钱？

查看试题解析
24. 某农户承包荒山若干亩，今年水果总产量为18000千克，此水果在市场上每千克售a元，在果园每千克售b元（b<a），该农户将水果拉到市场出售平均每天出售1000千克，需8人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．

(1)、分别用a，b表示两种方式出售水果的收入；

(2)、若a=1.3元，b=1.1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．

查看试题解析
25. 为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，不含后一个边界值）．

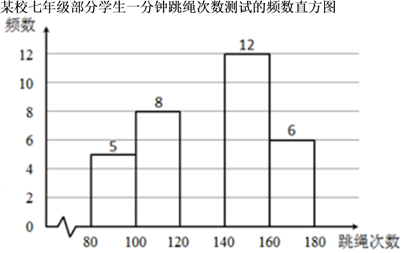(1)、参加测试的学生有多少人？

(2)、求 $a$ ， $b$ 的值，并把频数直方图补充完整．

(3)、若该年级共有 $320$ 名学生，估计该年级学生一分钟跳绳次数不少于 $120$ 次的人数．

查看试题解析
26. 甲、乙两支“徒步队”到野外沿相同路线徒步，徒步的路程为24千米．甲队步行速度为4千米/时，乙队步行速度为6千米/时．甲队出发1小时后，乙队才出发，同时乙队派一名联络员跑步在两队之间来回进行一次联络（不停顿），他跑步的速度为10千米/时．

(1)、乙队追上甲队需要多长时间？

(2)、联络员从出发到与甲队联系上后返回乙队时，他跑步的总路程是多少？

(3)、从甲队出发开始到乙队完成徒步路程时止，何时两队间间隔的路程为1千米？

查看试题解析
27. 如图，点O为直线AB上一点，过点O作射线OC，使∠BOC＝135°，将一个含45°角的直角三角尺的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边都在直线AB的下方．

(1)、将图1中的三角尺绕着点O逆时针旋转90°，如图2所示，此时∠BOM＝度（答案直接填写在答题卡的横线上）；在图2中，OM是否平分∠CON?请说明理由；

(2)、紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示，使得ON在∠AOC的内部，请探究：∠AOM与∠CON之间的数量关系，并说明理由；

(3)、将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，请你直接写出t的值为多少．

查看试题解析

品名	猕猴桃	芒果
批发价 $($ 元 $/$ 千克 $)$	20	40
零售价 $($ 元 $/$ 千克 $)$	26	50