湖南省株洲市醴陵市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2的相反数是（）

A、﹣2 B、0 C、2 D、4

查看试题解析
2. 如图所示，a和b的大小关系是（）

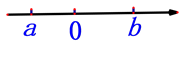A、a＞b B、a＜b C、2a=b D、2b=a

查看试题解析
3. 据统计，2019年醴陵高铁站年客运进出量约为237000人次.将237000用科学记数法表示为（）

A、 $23.7 \times 10^{4}$ B、 $2.37 \times 10^{5}$ C、 $2.37 \times 10^{6}$ D、 $23.7 \times 10^{5}$

查看试题解析
4. 下列不能表示“2a”的意义的是（）

A、2的a倍 B、a的2倍 C、2个a相加 D、2个a相乘

查看试题解析
5. 下列计算正确的是（　　）

A、-7-2=-5 B、 $a + 2 b = 3 a b$ C、 $3 a^{2} - 2 a^{2} = 1$ D、3xy-4yx=-xy

查看试题解析
6. 若6（y+2）=30，则y的值是（）

A、6 B、3 C、2 D、1

查看试题解析
7. 下列运用等式性质进行的变形，正确的是（　　）

A、如果a＝b，那么a+c＝b﹣c B、如果a²＝3a，那么a＝3 C、如果a＝b，那么 $\frac{a}{c} = \frac{b}{c}$ D、如果 $\frac{a}{c} = \frac{b}{c}$ ，那么a＝b

查看试题解析
8.
如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，则∠AOD等于（　　）

A、35° B、70° C、110° D、145°

查看试题解析
9. 若 $| a - 2 | = 2 - a$ ,则数a在数轴上的对应点在（）

A、表示数2的点的左侧 B、表示数2的点右侧 C、表示数2的点或表示数2的点的左侧 D、表示数2的点或表示数2的点的右侧

查看试题解析
10. 李明在做数学题时，发现下面计算是有规律结果：
3－2＝1；

8+7－6－5＝4

15+14+13－12－11－10＝9

24+23+22+21－20－19－18－17＝16. ……，

根据以上规律可知第20行左起第一个数是（）

A、400 B、401 C、440 D、441

查看试题解析

二、填空题

11. 如果把收入10元记为+10元，那么支出8元记为元

查看试题解析
12. 如果单项式 $- \frac{1}{2} x^{a} y$ 的次数为4，则a=

查看试题解析
13. 比a的倒数小n的数表示为

查看试题解析
14. 某校七年级为调查该年级400名学生一分钟跳绳次数成绩，打算从中随机抽取50人进行测试，则该问题中的样本容量为

查看试题解析
15. 若a是小于1的正数，则a, $\frac{1}{a}$ ,-a的大小关系用“<”连接起来

查看试题解析
16. 若 $| x - 2 | + {(3 y + 2)}^{2} = 0$ ,那么 $y^{x}$ 的值是

查看试题解析
17. 一个角的度数为 $28^{°} 34^{’}$ ，那么这个角的余角度数为

查看试题解析
18. 关于m、n的单项式 $2 m^{a} n^{b} 与 - 3 m^{2 (a - 1)} n$ 的和仍为单项式，则这个和为

查看试题解析

三、解答题

19. 计算： $- 1^{4} - \frac{1}{6} \times [2 - {(- 3)}^{2}]$

查看试题解析
20. 解方程： $\frac{4 x + 2}{5} - \frac{5 x - 7}{10} = 1$

查看试题解析
21. 在做解方程练习时，有一个方程“ $2 y - \frac{1}{2} = \frac{1}{2} y + �$ ”题中∎处不清晰，李明问老师，老师只是说：“∎是一个有理数，该方程的解与当X＝3时的整式 $5 (x - 1) - 2 (x - 2) - 4$ 的值相同。”依据老师的提示，请你帮李明求出方程的解，并找到这个有理数。

查看试题解析
22. 某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：

(1)、这次活动一共调查了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于多少度；

(4)、若该学校有1500人，请你估计该学校选择足球项目的学生人数约是多少人.

查看试题解析
23. 如图，一副三角饭的两个直角顶点重合在一起，

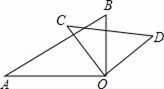(1)、比较大小：∠AOC∠BOD，理由是；

(2)、∠AOD与∠BOC的和为多少度？为什么？

查看试题解析
24. 阅读下列材料并填空

(1)、探究：平面上有n个点(n>2)且任意3个点不在同一条直线上，经过每两个点画一条直线，一共能画多少条直线?根据基本事实，我们知道两点确定一条直线，平面上有2个点时，可以画 $\frac{2 \times 1}{2} = 1$ 条直线，平面内有3个不在同一直线上点时，可画 $\frac{3 \times 2}{2} = 3$ 条直线，那么平面上有4个不在同一直线上的点时，可以画条，平面上有5个不在同一直线上的点时，可以画条，以此类推，平面上有n个不在同一直线上的点时，可以画条

(2)、运用：某足球比赛中有10个球队进行单循环比赛(每两队之间必须比赛一场)，一共进行多少场比赛?

查看试题解析
25. 已知点O是直线AB上的一点，∠COE= $90^{0}$ ，OF是∠AOE的平分线。

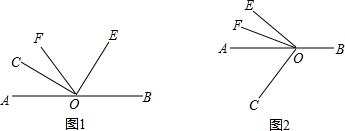(1)、当点C，E，F在直线AB的同侧(如图1所示)时.∠AOC= $38^{0}$ 时，求∠BOE和∠COF的度数，∠BOE和∠COF有什么数量关系?

(2)、当点C与点E，F在直线AB的两旁(如图2所示)时，∠AOC= $38^{0}$ ，(1)中∠BOE和∠COF的数量关系的结论是否成立?请给出你的结论并说明理由；

查看试题解析
26. 数轴上两个质点A．B所对应的数为−8、4，A．B两点各自以一定的速度在数轴上运动，且A点的运动速度为2个单位/秒。

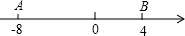(1)、点A．B两点同时出发相向而行，在4秒后相遇，求B点的运动速度；

(2)、A、B两点以(1)中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；

(3)、A、B两点以(1)中的速度同时出发，向数轴负方向运动，与此同时，C点从原点出发作同方向的运动，且在运动过程中，始终有CA=2CB，若干秒钟后，C停留在−10处，求此时B点的位置?

查看试题解析