山东省德州市德城区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 在- ,0,-|-5|,-0.6,2, ,-10中负数的个数有( )A、3 B、4 C、5 D、62. 下列计算正确的是A、 B、 C、 D、3. 据市旅游局统计,中秋小长假全市共接待中外游客32.51万人次,这个数字用科学记数法表示为( )A、 B、 C、 D、4. 如果有一个正方体,它的展开图可能是下列四个展开图中的
 A、
A、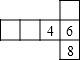 B、
B、 C、
C、 D、
D、 5. 小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km?设他家到学校的路程是xkm,则据题意列出的方程是( )A、 B、 C、 D、6. 钟表盘上指示的时间是10时40分,此刻时针与分针之间的夹角为( )A、 B、 C、 D、7. 如果点B在线段AC上,那么下列表达式中:①AB=
5. 小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km?设他家到学校的路程是xkm,则据题意列出的方程是( )A、 B、 C、 D、6. 钟表盘上指示的时间是10时40分,此刻时针与分针之间的夹角为( )A、 B、 C、 D、7. 如果点B在线段AC上,那么下列表达式中:①AB= AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( )
AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( ) A.1个 B.2个 C.3个 D.4个
A、1个 B、2个 C、3个 D、4个8. 关于x的方程a﹣3(x﹣5)=b(x+2)是一元一次方程,则b的取值情况是( )A、b≠﹣3 B、b=﹣3 C、b=﹣2 D、b为任意数9. 实数a、b在数轴上的位置如图,则 等于 A、2a B、2b C、 D、10. 下列说法中:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 与 是同类项,则 ;⑤若 、 互为相反数,那么 、 的商必等于 1;其中说法符合题意数有( )个.A、2 B、3 C、4 D、511. 6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A、2a B、2b C、 D、10. 下列说法中:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 与 是同类项,则 ;⑤若 、 互为相反数,那么 、 的商必等于 1;其中说法符合题意数有( )个.A、2 B、3 C、4 D、511. 6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( ) A、a=2b B、a=3b C、a=4b D、a=b12.
A、a=2b B、a=3b C、a=4b D、a=b12.如图,每个图形都由同样大小的矩形按照一定的规律组成,其中第①个图形的面积为6cm2 , 第②个图形的面积为18cm2 , 第③个图形的面积为36cm2 , …,那么第⑥个图形的面积为( )
 A、84cm2 B、90cm2 C、126cm2 D、168cm2
A、84cm2 B、90cm2 C、126cm2 D、168cm2二、填空题
-
13. 若 ,则 .14. 建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后在两个木桩之间拉一条线,建筑工人沿着拉紧的这条直线砌墙,这个事实说明的原理是 .15. 如果m是最大的负整数,n是绝对值最小的有理数,c是倒数等于它本身的自然数,那么代数式 的值为.16. 若关于 的代数式 中不含有二次项,则k =.17. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3h,若静水时船速为26km/h,水速为2km/h,则A港和B港相距km.18. 以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=17°,∠AOP的度数为.
三、解答题
-
19.(1)、计算:(2)、解方程: ;20. 已知 , .(1)、化简: ;(2)、已知 与 的同类项,求 的值.21. 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为 米,广场长为 米,宽为 米。
 (1)、请列式表示广场空地的面积;(2)、若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留 ).22. 如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数。
(1)、请列式表示广场空地的面积;(2)、若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留 ).22. 如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数。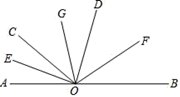 23. 已知关于 的方程 的解也是关于 的方程 的解.(1)、求 、 的值;(2)、若线段 ,在直线AB上取一点P,恰好使 ,点Q是PB的中点,求线段AQ的长.24. 为弘扬中华优秀文化传统,某中学在2014年元旦前夕,由校团委组织全校学生开展一次书法比赛,为了表彰在书法比赛中优秀学生,计划购买钢笔30支,毛笔20支,共需1070元,其中每支毛笔比钢笔贵6元.(1)、求钢笔和毛笔的单价各为多少元?(2)、①后来校团委决定调整设奖方案,扩大表彰面,需要购买上面的两种笔共60支(每种笔的单价不变).张老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领1322元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.
23. 已知关于 的方程 的解也是关于 的方程 的解.(1)、求 、 的值;(2)、若线段 ,在直线AB上取一点P,恰好使 ,点Q是PB的中点,求线段AQ的长.24. 为弘扬中华优秀文化传统,某中学在2014年元旦前夕,由校团委组织全校学生开展一次书法比赛,为了表彰在书法比赛中优秀学生,计划购买钢笔30支,毛笔20支,共需1070元,其中每支毛笔比钢笔贵6元.(1)、求钢笔和毛笔的单价各为多少元?(2)、①后来校团委决定调整设奖方案,扩大表彰面,需要购买上面的两种笔共60支(每种笔的单价不变).张老师做完预算后,向财务处王老师说:“我这次买这两种笔需支领1322元.”王老师算了一下,说:“如果你用这些钱只买这两种笔,那么帐肯定算错了.”请你用学过的方程知识解释王老师为什么说他用这些钱只买这两种笔的帐算错了.②张老师突然想起,所做的预算中还包括校长让他买的一支签字笔.如果签字笔的单价为不大于10元的整数,请通过计算,直接写出签字笔的单价可能为 元.
25. 如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.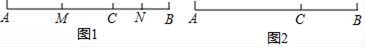 (1)、求线段MN的长度;(2)、根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;(3)、动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
(1)、求线段MN的长度;(2)、根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;(3)、动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?