山东省德州市宁津县2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 若|a|=﹣a,则a为( )A、a是负数 B、a是正数 C、a=0 D、负数或零2. 已知线段AB和点P,如果PA+PB=AB,那么下列结论一定正确是( )A、点P在线段AB上 B、点P为线段AB的中点 C、点P在线段AB外 D、点P在线段AB的延长线上3. 据相关报道,开展精准扶贫户工作五年来,我国约有5500万人摆脱贫困,国家发放扶贫资金共375亿元.将375亿用科学记数法表示为( )A、375×107 B、3.75×1010 C、3.75×109 D、37.5×1084. 下列四种说法,正确是( )A、—2ab的系数是-2 B、单项式a的系数是1、次数是0 C、 是二次单项式 D、π是一次单项式5. 有理数a、b、c在数轴上对应点位置如图所示,则下列关系式成立的是( )
 A、a+b+c<0 B、a+b+c>0 C、ab<ac D、bc>ab6. 一个角的补角比这个角的余角3倍还多10°,则这个角的度数为( )A、140° B、130° C、50° D、40°7. 当2<a<3时,代数式|3﹣a|﹣|2﹣a|的结果是( )A、﹣1 B、1 C、2a﹣5 D、5﹣2a8. 一商场某品牌服装统一按进价增加10%作为定价,元旦期间以9折促销.李老师在该摊位以198元的价格买了一件服装,则对于商家来说,这次生意的盈亏情况为( )A、亏2元 B、不亏不赚 C、赚2元 D、亏5元9. 两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )A、2cm B、4cm C、2cm或22cm D、4cm或44cm10. 将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )
A、a+b+c<0 B、a+b+c>0 C、ab<ac D、bc>ab6. 一个角的补角比这个角的余角3倍还多10°,则这个角的度数为( )A、140° B、130° C、50° D、40°7. 当2<a<3时,代数式|3﹣a|﹣|2﹣a|的结果是( )A、﹣1 B、1 C、2a﹣5 D、5﹣2a8. 一商场某品牌服装统一按进价增加10%作为定价,元旦期间以9折促销.李老师在该摊位以198元的价格买了一件服装,则对于商家来说,这次生意的盈亏情况为( )A、亏2元 B、不亏不赚 C、赚2元 D、亏5元9. 两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )A、2cm B、4cm C、2cm或22cm D、4cm或44cm10. 将下列如图的平面图形绕轴l旋转一周,可以得到的立体图形是( )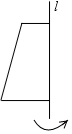 A、
A、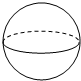 B、
B、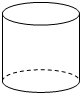 C、
C、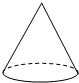 D、
D、 11. 已知一个多项式与3x2+8x的和等于3x2+2x+4,则这个多项式是( )A、6x+4 B、﹣6x+4 C、6x﹣4 D、﹣6x﹣412. 一项工程的施工现场,调来72名司机师傅参加挖土和运土工作,已知3名司机师傅挖出的土1名司机师傅恰好能开车全部运走,怎样分配这72名司机师傅才能使挖出的土能及时运走?可设派 名司机师傅挖士,其他的人运土,列方程:
11. 已知一个多项式与3x2+8x的和等于3x2+2x+4,则这个多项式是( )A、6x+4 B、﹣6x+4 C、6x﹣4 D、﹣6x﹣412. 一项工程的施工现场,调来72名司机师傅参加挖土和运土工作,已知3名司机师傅挖出的土1名司机师傅恰好能开车全部运走,怎样分配这72名司机师傅才能使挖出的土能及时运走?可设派 名司机师傅挖士,其他的人运土,列方程:上述所列方程,正确有___个
A、1 B、2 C、3 D、4二、填空题
-
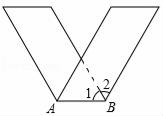
13. 在修建高速公路遇到大山的阻挡时,为了尽量缩短公路里程,往往需要开凿隧道,其所遵循的数学原理是 .14. 计算(﹣1)÷6×(﹣ )=.15. 已知|x|=5,y2=1,且 >0,则x﹣y= .16. 某潜艇从海平面以下27米上升到海平面以下18米,此潜艇上升了米.17. 已知|x|=3,y2=16,xy<0,则x﹣y= .18. 如图,一纸片沿直线AB折成的V字形图案,已知图中∠1=62°,则∠2的度数= .
三、解答题
-
19. 计算:(1)、2﹣23÷|﹣2|×(﹣7+5)(2)、20. 解方程:(1)、 ;(2)、 .21. 先化简,再求值.(1)、(2x+3y)﹣4y﹣(3x﹣2y),其中x=﹣3,y=2;(2)、(2a2b﹣4ab2)﹣2(﹣2ab2﹣a2b),其中a=1.b=﹣
 . 22. 历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)的形式来表示,把x等于某数a时的多项式的值用f(a)来表示,例如x=﹣1时,多项式f(x)=x2+3x﹣5的值记为f(﹣1),则f(﹣1)=﹣7.已知f(x)=ax5+bx3+3x+c,且f(0)=﹣1(1)、c= .(2)、若f(1)=2,求a+b的值;(3)、若f(2)=9,求f(﹣2)的值.23. ∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°.
. 22. 历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)的形式来表示,把x等于某数a时的多项式的值用f(a)来表示,例如x=﹣1时,多项式f(x)=x2+3x﹣5的值记为f(﹣1),则f(﹣1)=﹣7.已知f(x)=ax5+bx3+3x+c,且f(0)=﹣1(1)、c= .(2)、若f(1)=2,求a+b的值;(3)、若f(2)=9,求f(﹣2)的值.23. ∠AOB与∠COD有共同的顶点O,其中∠AOB=∠COD=60°. (1)、如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;(2)、如图①,若∠BOC=10°,求∠AOD的度数;(3)、如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;(4)、若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.24.(1)、观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(1)、如图①,试判断∠AOC与∠BOD的大小关系,并说明理由;(2)、如图①,若∠BOC=10°,求∠AOD的度数;(3)、如图①,猜想∠AOD与∠BOC的数量关系,并说明理由;(4)、若改变∠AOB,∠COD的位置,如图②,则(3)的结论还成立吗?若成立,请证明;若不成立,请直接写出你的猜想.24.(1)、观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段; (2)、模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的符合题意性;(3)、拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
(2)、模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的符合题意性;(3)、拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
25. 公园门票价格规定如下:
某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)、两个班各有多少个学生?(2)、如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?