四川省遂宁市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-02-17 类型：期末考试

进入出卷网下载

一、单选题

1. ${(- 3)}^{2}$ 的算术平方根是（）

A、9 B、3 C、 $\pm 3$ D、-3

查看试题解析
2. 立方根等于它本身的有（）

A、0,1 B、-1,0,1 C、0, D、1

查看试题解析
3. 在下列实数 $\frac{22}{7}$ ，3.14159， $\sqrt{12}$ ，0， $\frac{π}{2}$ ， $\sqrt{64}$ ，0.131131113…， $\sqrt[3]{9}$ ，中，无理数有（　　）个．

A、3 B、4 C、5 D、6

查看试题解析
4. 如图，已知 $A B = A C$ ，则数轴上 $C$ 点所表示的数为（）

A、 $- \sqrt{3}$ B、 $- \sqrt{5}$ C、 $1 - \sqrt{3}$ D、 $1 - \sqrt{5}$

查看试题解析
5. 在实数 $- \sqrt{2}$ ，3，0，0.5中，最小的数是（）

A、 $- \sqrt{2}$ B、3 C、0 D、0.5

查看试题解析
6. 下列计算中正确是（）

A、 $b^{3} \cdot b^{2} = b^{6}$ B、 $x^{3} + x^{3} = x^{6}$ C、 $a^{2} \cdot a^{2} = 0$ D、 ${(- a^{3})}^{2} = a^{6}$

查看试题解析
7. 若 $(x^{2} - p x + q) (x - 3)$ 展开后不含 $x$ 的一次项，则 $p$ 与 $q$ 的关系是（）

A、 $p = 3 q$ B、 $q + 3 p = 0$ C、 $p + 3 q = 0$ D、 $q = 3 p$

查看试题解析
8. 下列多项式相乘，不能用平方差公式计算的是（）

A、(x＋3y)(x－3y) B、(－2x＋3y)(－2x－3y) C、(x－2y)(2y＋x) D、(2x－3y)(3y－2x)

查看试题解析
9. 若方程 $x^{2} + k x + 64 = 0$ 的左边是完全平方式，则 $k$ 的值为（）

A、16 B、 $\pm 8$ C、 $- 16$ D、 $\pm 16$

查看试题解析
10. 下列各式从左到右的变形是分解因式的是（）

A、 $2 a^{2} - b^{2} = (a + b) (a - b) + a^{2}$ B、 $2 a (b + c) = 2 a b + 2 a c$ C、 $x^{3} - 2 x^{2} + x = x {(x - 1)}^{2}$ D、 $x^{2} + x = x^{2} (1 + \frac{1}{x})$

查看试题解析
11. 如果二次三项式 $x^{2} + a x + 2$ 可分解为 $(x - 1) (x + b)$ ，则 $a + b$ 的值为（）

A、 $- 2$ B、 $- 5$ C、3 D、5

查看试题解析
12. 下列说法正确是（）

A、 $\sqrt{16}$ 的算术平方根是2 B、无限小数都是无理数 C、0.720精确到了百分位 D、真命题的逆命题都是真命题

查看试题解析
13. 下列各组数据分别为三角形的三边长，不能组成直角三角形的是（）

A、9，12，15 B、7，24，25 C、6，8，10 D、3，5，7

查看试题解析
14. 用反证法证明：“三角形三内角中至少有一个角不大于60°”时，第一步应是（）

A、假设三角形三内角中至多有一个角不大于60° B、假设三角形三内角中至少有一个角不小于60° C、假设三角形三内角都大于60° D、假设三角形三内角中至少有一个角大于60°

查看试题解析
15. 2009年，我国粮食总产量54000万吨，其中，谷物49000万吨，豆类2700万吨，薯类2300万吨。如果用扇形图表示这组数据，问豆类这部分扇形的圆心角为多少度（）

A、16° B、18° C、20° D、22°

查看试题解析
16. 如图，在△ABC中，DE是边AC的垂直平分线，AE＝5cm，△ABD的周长为26cm，则△ABC的周长为（）

A、29 B、32 C、36 D、38

查看试题解析
17. 如图，开口玻璃罐长、宽、高分别为16、6和6，在罐內点E处有一小块饼干碎末，此时一只蚂蚁正好在罐外长方形ABCD的中心H处，蚂蚁到达饼干的最短距离是多少（）

A、 $\sqrt{277}$ B、17 C、 $\sqrt{205}$ D、 $\sqrt{145}$

查看试题解析
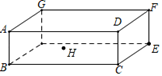18. 如图，在△ABC中，高AD和BE交于点H，且∠1＝∠2＝22.5°，下列结论正确有（　　）

①∠1＝∠3；②BD+DH＝AB；③2AH＝BH；④若CD＝ $\sqrt{2}$ ，则BH＝3；⑤若DF⊥BE于点F，则AE－DF＝FH．

A、①②④ B、①②⑤ C、②③④ D、③④⑤

查看试题解析

二、填空题

19. 已知 $\sqrt{5}$ 的小数部分是a， $\sqrt{7}$ 的整数部分是b，则a+b＝．

查看试题解析
20. 若x、y为实数，且 ${(a + \sqrt{3})}^{2} + \sqrt{b - 2}$ ＝0，则a^b的值＝

查看试题解析
21. 若 $3^{a} = 2$ ， $3^{b} = 5$ ，则 $3^{3 a - 2 b} =$ ．

查看试题解析
22. 多项式15a²b²+5a²b﹣20a²b²中各项的公因式是．

查看试题解析
23. 如图，△ACE≌△DBF，如果∠E＝∠F，DA＝12，CB＝2，那么线段AB的长是．

查看试题解析
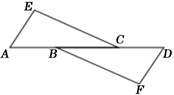24. 一次跳远中，成绩在4.05米以上的人有8人，频率为0.4，则参加比赛的运动员共有人.

查看试题解析
25. 如图，在△ABC中，∠ABC＜∠BCA＜∠BAC，∠BAC和∠ABC的外角平分线AE、BD分别与BC、CA的延长线交于E、D．若AB＝AE，BD＝BA．则∠BCA的度数为．

查看试题解析

三、解答题

26. 计算： ${(- 1)}^{3} + | 1 - \sqrt{2} | + \sqrt[3]{8} - \sqrt{{(- 2)}^{2}}$

查看试题解析
27. 分解因式： $2 x^{2} (x - y) + 2 (y - x)$ ．

查看试题解析
28. 先化简,再求值： $[(2 a + b) (2 a - b) - {(2 a - b)}^{2} - b (a - 2 b)] \div (2 a)$ ,其中 $a = \frac{1}{2020}$ ， $b = \frac{2}{3}$ ．

查看试题解析
29. 如图所示，已知锐角∠AOB及一点P．

(1)、过点P作OA、OB的垂线，垂足分别是M、N；（只作图，保留作图痕迹，不写作法）

(2)、猜想∠MPN与∠AOB之间的关系，并证明．

查看试题解析
30. 为了解市民对“垃圾分类知识”的知晓程度，某数学学习兴趣小组对市民进行随机抽样的问卷调查，调查结果分为“ $A$ .非常了解”、“ $B$ .了解”、“ $C$ .基本了解”、“ $D$ .不太了解”四个等级进行统计，并将统计结果绘制成如下两幅不完整的统计图(图1，图2)，请根据图中的信息解答下列问题.

(1)、这次调查的市民人数为人，图2中， $n =$ ；

(2)、补全图1中的条形统计图；

(3)、在图2中的扇形统计图中，求“ $C$ .基本了解”所在扇形的圆心角度数；

(4)、据统计，2018年该市约有市民500万人，那么根据抽样调查的结果，可估计对“垃圾分类知识”的知晓程度为“ $D$ .不太了解”的市民约有多少万人？

查看试题解析
31. 为了积极响应国家新农村建设，遂宁市某镇政府采用了移动宣讲的形式进行宣传动员．如图，笔直公路MN的一侧点A处有一村庄，村庄A到公路MN的距离为600米，假使宣讲车P周围1000米以内能听到广播宣传，宣讲车P在公路MN上沿PN方向行驶时：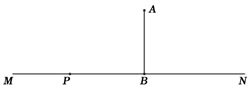

(1)、请问村庄能否听到宣传，请说明理由；

(2)、如果能听到，已知宣讲车的速度是200米/分钟，那么村庄总共能听到多长时间的宣传？

查看试题解析
32. 在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

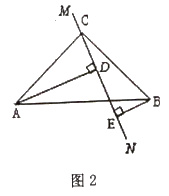(1)、当直线MN绕点C旋转到图1的位置时，△ADC和△CEB全等吗?请说明理由.

(2)、聪明的小亮发现，当直线MN绕点C旋转到图1的位置时，可得DE＝AD＋BE，请你说明其中的理由。

(3)、小亮将直线MN绕点C旋转到图2的位置，线段DE、AD、BE之间存在着什么的数量关系，请写出这一关系，并说明理由.

查看试题解析
33. 如图，在△ABC中，∠C＝90°，AB的垂直平分线DE交AC于点E，垂足是D，F是BC上一点，EF平分∠AFC，EG⊥AF于点G．

(1)、试判断EC与EG，CF与GF是否相等；（直接写出结果，不要求证明）

(2)、求证：AG＝BC；

(3)、若AB＝5，AF+BF＝6，求EG的长．

查看试题解析