四川省成都市邛崃市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 从实数0.4, ,0, , ,3.1415926中选出两个无理数是( )A、 , B、 , C、3.1415926, D、 ,2. 若二次根式 有意义,则x的取值范围为( )A、x≥ B、x≤- C、x≥- D、x≤3. 下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
A、 B、
B、 C、
C、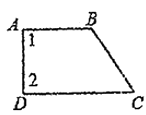 D、
D、 4. 在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( )A、(-3,2) B、(2,3) C、(2,-3) D、(-2,-3)5. 射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.62,S丙2=0.48,S丁2=0.45,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁6. 不等式组 的解集在数轴上表示正确是( )A、
4. 在平面直角坐标系中,点P与点M关于y轴对称,点N与点M关于x轴对称,若点P的坐标为(-2,3),则点N的坐标为( )A、(-3,2) B、(2,3) C、(2,-3) D、(-2,-3)5. 射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为S甲2=0.51,S乙2=0.62,S丙2=0.48,S丁2=0.45,则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁6. 不等式组 的解集在数轴上表示正确是( )A、 B、
B、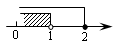 C、
C、 D、
D、 7. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
7. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )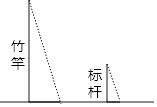 A、五丈 B、四丈五尺 C、一丈 D、五尺8. 甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
A、五丈 B、四丈五尺 C、一丈 D、五尺8. 甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( ) A、甲地气温的中位数是6℃ B、两地气温的平均数相同 C、乙地气温的众数是8℃ D、乙地气温相对比较稳定9. 下列说法错误的是( )A、打开电视机,正在播放广告这一事件是随机事件 B、要了解小赵一家三口的身体健康状况,适合采用抽样调查 C、方差越大,数据的波动越大 D、样本中个体的数目称为样本容量10. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、
A、甲地气温的中位数是6℃ B、两地气温的平均数相同 C、乙地气温的众数是8℃ D、乙地气温相对比较稳定9. 下列说法错误的是( )A、打开电视机,正在播放广告这一事件是随机事件 B、要了解小赵一家三口的身体健康状况,适合采用抽样调查 C、方差越大,数据的波动越大 D、样本中个体的数目称为样本容量10. 如图,一次函数y=mx+n与y=mnx(m≠0,n≠0)在同一坐标系内的图象可能是( )A、 B、
B、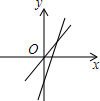 C、
C、 D、
D、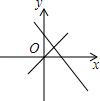
二、填空题
-
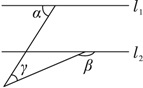
11. 在平面直角坐标系中,点 一定在第象限.12. 如图,l1∥l2 , 则 .
 13. 在Rt△ABC中,AC=9,BC=12,则AB2=;14. 如图,根据函数图象回答问题:方程组 的解为.
13. 在Rt△ABC中,AC=9,BC=12,则AB2=;14. 如图,根据函数图象回答问题:方程组 的解为. 15. 比较大小: (填“>”、“<”或“=”).16. 中国古代的数学专著《九章算术》有方程组问题“五只雀,六只燕,共重1斤(等于16两),雀重燕轻.互换其中一只,恰好一样重.”设每只雀、燕的重量各为x两,y两,则根据题意,可得方程组为 .17. 如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
15. 比较大小: (填“>”、“<”或“=”).16. 中国古代的数学专著《九章算术》有方程组问题“五只雀,六只燕,共重1斤(等于16两),雀重燕轻.互换其中一只,恰好一样重.”设每只雀、燕的重量各为x两,y两,则根据题意,可得方程组为 .17. 如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .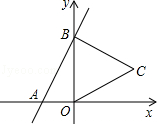 18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a、b的代数式表示).
18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a、b的代数式表示).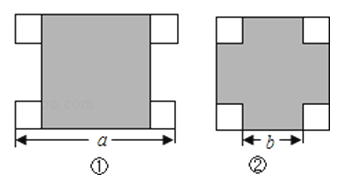
三、解答题
-
19.(1)、计算:(2)、求满足不等式组 的所有整数解.20. 解方程组: .21. 已知当 时,代数式 的值为17.(1)、若关于y的方程2my+n=4-ny-m的解为y=2,求mn的值;(2)、若规定 表示不超过a的最大整数,例如[4.3]=4,请在此规定下求 的值.22. 如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
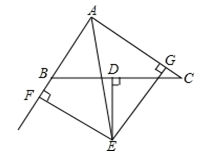
求证:
(1)、BF=CG;(2)、AF= (AB+AC).23. 某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:20
21
19
16
27
18
31
29
21
22
25
20
19
22
35
33
19
17
18
29
18
35
22
15
18
18
31
31
19
22
整理上面数据,得到条形统计图:
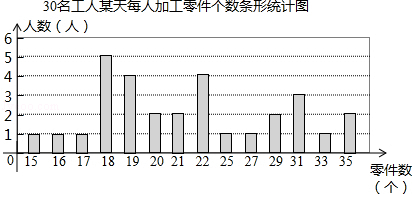
样本数据的平均数、众数、中位数如下表所示:
统计量
平均数
众数
中位数
数值
23
m
21
根据以上信息,解答下列问题:
(1)、上表中众数m的值为;(2)、为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)(3)、该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.24. 如图,直线 的解析式为 ,且 与 轴交于点D,直线 经过点 、 ,直线 、 交于点C. (1)、求直线 的解析表达式;(2)、求 的面积;(3)、在直线 上存在异于点C的另一点P,使得 与 的面积相等,请求出点P的坐标.25. 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠得到△GBE,且点G在矩形ABCD内部.将BG延长交DC于点F,若DC=nDF,则 为?
(1)、求直线 的解析表达式;(2)、求 的面积;(3)、在直线 上存在异于点C的另一点P,使得 与 的面积相等,请求出点P的坐标.25. 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠得到△GBE,且点G在矩形ABCD内部.将BG延长交DC于点F,若DC=nDF,则 为?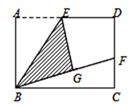 26. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.27. 已知:方程组 的解x为非正数,y为负数.(1)、求a的取值范围;(2)、化简|a-3|+|a+2|;(3)、在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.28. 如图,直线y=﹣ x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
26. 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.(1)、求每辆大客车和每辆小客车的乘客座位数;(2)、由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.27. 已知:方程组 的解x为非正数,y为负数.(1)、求a的取值范围;(2)、化简|a-3|+|a+2|;(3)、在a的取值范围中,当a为何整数时,不等式2ax+x>2a+1的解为x<1.28. 如图,直线y=﹣ x+6分别与x轴、y轴交于A、B两点;直线y= x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒). (1)、求点C的坐标.(2)、当0<t<5时,求S与t之间的函数关系式,并求S的最大值。(3)、当t>0时,直接写出点(5,3)在正方形PQMN内部时t的取值范围。
(1)、求点C的坐标.(2)、当0<t<5时,求S与t之间的函数关系式,并求S的最大值。(3)、当t>0时,直接写出点(5,3)在正方形PQMN内部时t的取值范围。