山东省威海市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 不论x取何值,下列分式始终有意义的是( )A、 B、 C、 D、2. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 一个多边形的内角和比外角和多540°,这个多边形为( )A、五边形 B、六边形 C、七边形 D、八边形4. 某次数学测试中,八年级一班平均分为80分,八年级二班的平均分为82分,下列说法错误的是( )A、两个班的平均分为81分 B、两个班的平均分不可能高于82分 C、若一班的人数比二班多,则两个班的平均分低于81分 D、若两个班的人数相同,则两个班的平均分为81分5. 下列变形正确是( )A、 = B、 = C、 = D、 =6. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种7. 一组数据0,1,2,2,3,4,若添加一个数据2,则下列统计量中发生变化的是( )A、方差 B、中位数 C、平均数 D、极差8. 如图,若将线段AB平移至A1B1 , 则a+b的值为( )
3. 一个多边形的内角和比外角和多540°,这个多边形为( )A、五边形 B、六边形 C、七边形 D、八边形4. 某次数学测试中,八年级一班平均分为80分,八年级二班的平均分为82分,下列说法错误的是( )A、两个班的平均分为81分 B、两个班的平均分不可能高于82分 C、若一班的人数比二班多,则两个班的平均分低于81分 D、若两个班的人数相同,则两个班的平均分为81分5. 下列变形正确是( )A、 = B、 = C、 = D、 =6. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种7. 一组数据0,1,2,2,3,4,若添加一个数据2,则下列统计量中发生变化的是( )A、方差 B、中位数 C、平均数 D、极差8. 如图,若将线段AB平移至A1B1 , 则a+b的值为( ) A、﹣3 B、3 C、﹣2 D、09. 某项工作,甲单独完成需要40分钟;若甲、乙共同做20分钟后,乙需再单独做20分钟才能完成,则乙单独完成需要( )A、40分钟 B、60分钟 C、80分钟 D、100分钟10. 如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
A、﹣3 B、3 C、﹣2 D、09. 某项工作,甲单独完成需要40分钟;若甲、乙共同做20分钟后,乙需再单独做20分钟才能完成,则乙单独完成需要( )A、40分钟 B、60分钟 C、80分钟 D、100分钟10. 如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
 A、甲正确,乙错误 B、乙正确,甲错误 C、甲、乙均正确 D、甲、乙均错误11. 如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确有( )
A、甲正确,乙错误 B、乙正确,甲错误 C、甲、乙均正确 D、甲、乙均错误11. 如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确有( )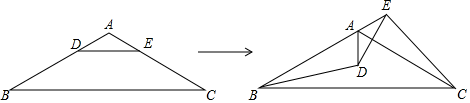 A、②③ B、②③④ C、①②③ D、①②③④
A、②③ B、②③④ C、①②③ D、①②③④二、解答题
-
12. 如果a2+2a-1=0,求代数式 的值.13. 因式分解:(1)、xy2﹣8xy+12x(2)、9x2﹣6x(x+2y)+(x+2y)214. 计算:(1)、(2)、( +x﹣2)÷15. 某工厂甲、乙两个车间各有工人200人,为了解这两个车间工人的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据从甲、乙两个车间各抽取20名工人进行生产技能测试,测试成绩如下:
甲:78 86 74 85 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙:93 67 88 81 72 81 94 83 77 83 80 81 64 81 73 78 82 80 70 52
整理数据按如下分数段整理、描述这两组样本数据:
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤99
甲
0
11
1
乙
1
2
5
10
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
平均数
中位数
众数
甲
77.5
75
乙
78
得出结论可以推断车间工人的生产技能水平较高,理由为.(至少从两个角度说明推断的合理性)
16. 线段AB,CD在正方形网格中的位置如图所示,将线段AB绕点O按顺时针方向旋转一定角度α,可以得到线段CD.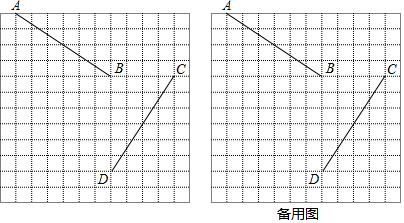 (1)、请在下图中画出点O;(2)、若点A、B、C、D的坐标分别为A(﹣5,5)、B(1,1)、C(5,1)、D(1,﹣5),则点O的坐标为.(3)、α=.17. 小明家距学校2000米,某天他步行去上学,走到路程的一半时发现忘带作业,此时离上课时间还有25分钟,于是他立刻步行回家取,随后骑车返回学校,在上课前5分钟到达了学校.若小明骑车的平均速度是步行速度的5倍,求小明步行的平均速度.18. 如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)、请在下图中画出点O;(2)、若点A、B、C、D的坐标分别为A(﹣5,5)、B(1,1)、C(5,1)、D(1,﹣5),则点O的坐标为.(3)、α=.17. 小明家距学校2000米,某天他步行去上学,走到路程的一半时发现忘带作业,此时离上课时间还有25分钟,于是他立刻步行回家取,随后骑车返回学校,在上课前5分钟到达了学校.若小明骑车的平均速度是步行速度的5倍,求小明步行的平均速度.18. 如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD. (1)、将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.(2)、若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.19. 已知,△ABC,AD⊥BD于点D,AE⊥CE于点E,连接DE.
(1)、将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.(2)、若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.19. 已知,△ABC,AD⊥BD于点D,AE⊥CE于点E,连接DE. (1)、如图1,若BD,CE分别为△ABC的外角平分线,求证:DE= (AB+BC+AC).(2)、如图2,若BD,CE分别为△ABC的内角平分线,(1)中的结论成立吗?若成立请说明理由;若不成立,请猜想出新的结论并证明;(3)、如图3,若BD,CE分别为△ABC的一个内角和一个外角的平分线,AB=8,BC=10,AC=7,请直接写出DE的长为.
(1)、如图1,若BD,CE分别为△ABC的外角平分线,求证:DE= (AB+BC+AC).(2)、如图2,若BD,CE分别为△ABC的内角平分线,(1)中的结论成立吗?若成立请说明理由;若不成立,请猜想出新的结论并证明;(3)、如图3,若BD,CE分别为△ABC的一个内角和一个外角的平分线,AB=8,BC=10,AC=7,请直接写出DE的长为.三、填空题
-
20. (-2)2018+(-2)2019=.21. 如图,在平面直角坐标系xOy中,△COD可以看作是△AOB经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△AOB得到△COD的过程:.
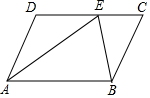
 22. 如图,在▱ABCD中,∠D=120°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.
22. 如图,在▱ABCD中,∠D=120°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为.